
已知A、B为抛物线C:y2 = 4x上的两个动点,点A在第一象限,点B在第四象限l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.
(Ⅰ)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;
(Ⅱ)设C、D为直线l1、l2与直线x = 4的交点,求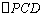 面积的最小值.
面积的最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1(n∈N*).
(1)求a1,a2;
(2)猜想数列{Sn}的通项公式,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
若两条异面直线所成的角为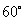 ,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有
,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有
A.12对 B.18对 C.24 对 D.30对
查看答案和解析>>
科目:高中数学 来源: 题型:
若三个非零且互不相等的实数a、b、c满足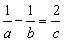 ,则称a、 b、c是调和的;若满a + c = 2b足,则称a、b、c是等差的.若集合P中元素a、b、c既是调和的,又是等差的,则称集合P为“好集”.若集合
,则称a、 b、c是调和的;若满a + c = 2b足,则称a、b、c是等差的.若集合P中元素a、b、c既是调和的,又是等差的,则称集合P为“好集”.若集合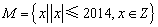 ,集合
,集合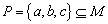 .则
.则
(1)“好集” P中的元素最大值为 ;
(2)“好集” P的个数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
将2名教师6名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和3名学生组成,不同的安排方案共有
(A)240种 (B)120种 (C)40种 (D)20种
查看答案和解析>>
科目:高中数学 来源: 题型:
某学校从高二甲、乙两个班中各选6名同学参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则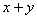 的值为
的值为
A.6 B. 7 C.8 D.9

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com