
例
已知椭圆C:![]() 上动点
上动点![]() 到定点
到定点![]() ,其中
,其中![]() 的距离
的距离![]() 的最小值为1.(1)请确定M点的坐标(2)试问是否存在经过M点的直线
的最小值为1.(1)请确定M点的坐标(2)试问是否存在经过M点的直线![]() ,使
,使![]() 与椭圆C的两个交点A、B满足条件
与椭圆C的两个交点A、B满足条件![]() (O为原点),若存在,求出
(O为原点),若存在,求出![]() 的方程,若不存在请说是理由。
的方程,若不存在请说是理由。
(1,0);这样的直线不存在。
【思维分析】此题解题关键是由条件![]() 知
知![]() 从而将条件转化点的坐标运算再结合韦达定理解答。
从而将条件转化点的坐标运算再结合韦达定理解答。
解析:设![]() ,由
,由![]() 得
得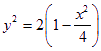 故
故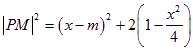
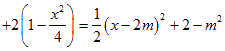 由于
由于![]() 且
且![]() 故当
故当![]() 时,
时,![]() 的最小值为
的最小值为![]() 此时
此时![]() ,当
,当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() 解得
解得![]() 不合题意舍去。综上所知当
不合题意舍去。综上所知当![]() 是满足题意此时M的坐标为(1,0)。
是满足题意此时M的坐标为(1,0)。
(2)由题意知条件![]() 等价于
等价于![]() ,当
,当![]() 的斜率不存在时,
的斜率不存在时,![]() 与C的交点为
与C的交点为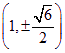 ,此时
,此时![]() ,设
,设![]() 的方程为
的方程为![]() ,代入椭圆方程整理得
,代入椭圆方程整理得![]() ,由于点M在椭圆内部故
,由于点M在椭圆内部故![]() 恒成立,由
恒成立,由![]() 知
知![]() 即
即![]() ,据韦达定理得
,据韦达定理得![]() ,
,![]() 代入上式得
代入上式得![]() 得
得![]() 不合题意。综上知这样的直线不存在。
不合题意。综上知这样的直线不存在。
【知识点归类点拔】在解题过程中要注意将在向量给出的条件转化向量的坐标运算,从而与两交点的坐标联系起来才自然应用韦达定理建立起关系式。此题解答具有很强的示范性,请同学们认真体会、融会贯通。


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com