
设函数 ,其中,角
,其中,角 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点 ,且
,且 .
.
(1)若 点的坐标为(-
点的坐标为(- ),求
),求 的值;
的值;
(2)若点 为平面区域
为平面区域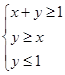 上的一个动点,试确定角
上的一个动点,试确定角 的取值范围,并求函数
的取值范围,并求函数 的值域.
的值域.
科目:高中数学 来源: 题型:解答题
某企业生产A,B两种产品,生产每吨产品所需的劳动力和煤、电耗如下表:
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360 t,并且供电局只能供电200 kW,试问该企业生产A,B两种产品各多少吨,才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司承担了每天至少搬运280吨水泥的任务,已知该公司有6辆A型卡车和8辆B型卡车.又已知A型卡车每天每辆的运载量为30吨,成本费为0.9千元;B型卡车每天每辆的运载量为40吨,成本费为1千元.
(1)如果你是公司的经理,为使公司所花的成本费最小,每天应派出A型卡车、B型卡车各多少辆?
(2)在(1)的所求区域内,求目标函数 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列各函数中,最小值为2的是 ( )
A.y=x+ |
B.y= |
| C.y=logax+logxa(a>0,x>0且a≠1,x≠1) |
| D.y=3-x+3x(x>0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com