分析:由题意,方程左边对应的函数图象是以原点为圆心、半径为1的圆的上半圆,右边对应的函数图象是经过定点C(0,2)且斜率为k的一条直线.可得当直线与半圆相切时或直线在x轴上的交点位于(-1,0)和(1,0)之间时,原方程有唯一的实数解.由此建立关于k的代数关系式,即可得到实数k的范围.
解答:解:
设y
1=
,
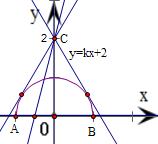
表示以原点为圆心、半径为1的圆的上半圆(含端点A、B)
设y
2=kx+2,表示经过定点C(0,2)且斜率为k的一条直线
当直线y
2=kx+2与半圆y
1=
相切时,原方程有唯一解
此时原点到直线的距离等于1,得
=1,解之得k=
±当直线在x轴上的交点位于A、B之间时,原方程也有唯一解
∵k
AC=2且k
BC=-2,
∴线在x轴上的交点位于A、B之间时,k<-2或k>2
综上所述,原方程有唯一实数解时,k<-2或k>2或k=
±故选:D
点评:本题给出方程有唯一的实数解,求参数k的值或范围.着重考查了直线方程、圆的方程和直线与圆的位置关系等知识,属于中档题.

 设y1=
设y1=

 名校课堂系列答案
名校课堂系列答案