Question

（06年天津卷理）（14分）

如图，以椭圆的中心O为圆心，分别以和为半径作大圆和小圆。过椭圆右焦点作垂直于轴的直线交大圆于第一象限内的点A。连结OA交小圆于点B。设直线BF是小圆的切线。

  

（I）证明并求直线BF与同的交点M的坐标；

（II）设直线BF交椭圆P、Q两点，证明

Answer 1

解析：（I）证明：由题设条件知，故

                     即

       因此，　　　　①

       在中，

       于是，直线OA的斜率设直线BF的斜率为则

                    

       这时，直线BF的方程为令则

       所以直线BF与轴的交点为

 

（II）证明：由（I），得直线的方程为且

                     　　　　　　②

       由已知，设、则它们的坐标满足方程组

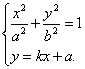                     　　　　　　　　③

       由方程组③消去并整理得

                     　　　④

       由式①、②和④，

                    

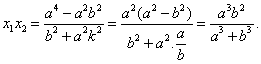
       由方程组③消去并整理得

                     　　⑤

       由式②和⑤，

                    

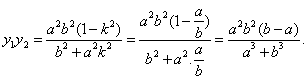
       综上，得到

                    

       注意到得

                    

　　　　　　　　　

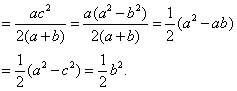
【高考考点】椭圆的标准方程和几何性质　直线方程　平面向量　曲线和方程的关系

【易错点】：不能找出隐含条件结合完成第一问证明，第二问到的计算及向结论的化简过程

【备考提示】：掌握椭圆的几何性质，善于找出已知中的隐含条件是解决此题的关键