
给出下列说法:
(1)方程 的解集为{2,-2};
的解集为{2,-2};
(2)集合 与{y|y=x-1,xÎ
R}的公共元素所组成的集合为{0,-1};
与{y|y=x-1,xÎ
R}的公共元素所组成的集合为{0,-1};
(3)集合{x|x-1<0}与集合{x|x>a aÎ R}没有公共元素.其中正确的个数为
[ ]
|
A.0 |
B.1 |
C.2 |
D.3 |
|
要判断这些命题的真假,这就需要对用来描述的这些命题的集合语言进行转化,以弄清集合的构成.在 (1)中方程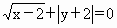 等价于 等价于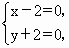 即 即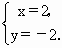 其解应为有序实数时,因此其解集应为{(2,-2)},故命题(1)是假命题,而在(2)中,由于集合 其解应为有序实数时,因此其解集应为{(2,-2)},故命题(1)是假命题,而在(2)中,由于集合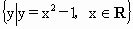 的代表元素是y,而y满足属性:“ 的代表元素是y,而y满足属性:“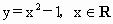 ”,由于当xÎ
R时, ”,由于当xÎ
R时,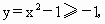 所以集合 所以集合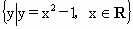 是由大于或等于-1的实数所组成的集合,同理{y|y=x-1,xÎ
R}是R,因此(2)也是错误的.在(3)中,集合{x|x-1<0},即为不等式x-1<0,即x<1的解集,而{x|x>a,aÎ
R}即为不等式x>a的解集.由图可知,这两个集合可能有公共的元素,也可能没有公共的元素,因此(3)也是错误的.故答案为A. 是由大于或等于-1的实数所组成的集合,同理{y|y=x-1,xÎ
R}是R,因此(2)也是错误的.在(3)中,集合{x|x-1<0},即为不等式x-1<0,即x<1的解集,而{x|x>a,aÎ
R}即为不等式x>a的解集.由图可知,这两个集合可能有公共的元素,也可能没有公共的元素,因此(3)也是错误的.故答案为A.
|


科目:高中数学 来源: 题型:
| a2+b2 |
| b |
| a-1 |
| 5 |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:013
给出下列说法:
(1)
方程 的解集为{2,-2};
的解集为{2,-2};
(2)
集合 与{y|y=x-1,xÎR}的公共元素所组成的集合为{0,-1};
与{y|y=x-1,xÎR}的公共元素所组成的集合为{0,-1};
(3)
集合{x|x-1<0}与集合{x|x>a aÎR}没有公共元素.其中正确的个数为[
]|
A .0 |
B .1 |
C .2 |
D .3 |
查看答案和解析>>
科目:高中数学 来源:设计必修四数学人教A版 人教A版 题型:022
给出下列说法:
(1)在△ABC中,若![]() <0,则△ABC是锐角三角形;
<0,则△ABC是锐角三角形;
(2)在△ABC中,若![]() >0,则△ABC是钝角三角形;
>0,则△ABC是钝角三角形;
(3)△ABC是直角三角形![]() =0;
=0;
(4)△ABC是斜三角形的必要不充分条件是![]() .
.
其中,正确的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列说法:
1存在实数![]() ,使
,使![]() ;
;
2若![]() 是锐角三角形的内角,则
是锐角三角形的内角,则![]() ;
;
3为了得到函数y=sin的图象,只需把函数y=sin的图象向右平移![]() 个长度单位;
个长度单位;
4 函数![]() 的最小正周期为
的最小正周期为![]() ;
;
5在![]() 中,若
中,若![]() ,则A=B。其中正确说法的序号是 。
,则A=B。其中正确说法的序号是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com