已知三角形的三条边长构成等比数列,他们的公比为q,则q的取值范围是 .
【答案】
分析:设三边:a、aq、aq
2、q>0,则由三边关系:两短边和大于第三边,分q≥1和q<1两种情况分别求得q的范围,最后综合可得答案.
解答:解:设三边:a、aq、aq
2、q>0,则由三边关系:两短边和大于第三边可得
(1)当q≥1时,aq
2为最大边,a+aq>aq
2,等价于:q
2-q-1<0,由于方程q
2-q-1=0两根为:

和
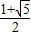
,
故得解:
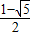
<q<
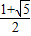
∵q≥1,
∴1≤q<
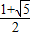
(2)当0<q<1时,a为最大边,aq+aq
2>a,即得q
2+q-1>0,解之得q>
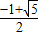
或q<-
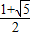
∵0<q<1
∴1>q>
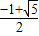
综合(1)(2),得:q∈(
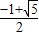
,
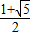
)
故答案为:(
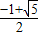
,
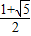
)
点评:本题以三角形为载体,考查等比数列,考查解不等式,同时考查了分类讨论的数学思想.

 和
和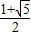 ,
,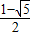 <q<
<q<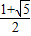
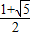
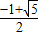 或q<-
或q<-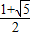
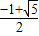
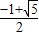 ,
,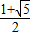 )
)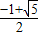 ,
,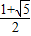 )
)

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案