
设0≤θ≤2π时,已知两个向量=(cosθ,sinθ),=(2+sinθ,2-cosθ),则向量长度的最大值是 ( )
A. B. C.3 D.2
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
| 1 |
| 6 |
| ln2 |
| 2! |
| ln3 |
| 3! |
| lnn |
| n! |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a+2e | x |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市高三上学期期末模拟文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
在平面直角坐标系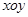 中,已知三点
中,已知三点 ,
,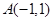 ,
,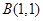 ,曲线C上任意—点
,曲线C上任意—点 满足:
满足: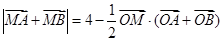 .
.
(l)求曲线C的方程;
(2)设点P是曲线C上的任意一点,过原点的直线L与曲线相交于M,N两点,若直线PM,PN的斜率都存在,并记为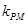 ,
,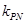 .试探究
.试探究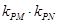 的值是否与点P及直线L有关,并证明你的结论;
的值是否与点P及直线L有关,并证明你的结论;
(3)设曲线C与y轴交于D、E两点,点M (0,m)在线段DE上,点P在曲线C上运动.若当点P的坐标为(0,2)时,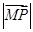 取得最小值,求实数m的取值范围.
取得最小值,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com