
(2)已知A=60°,a=7,b=5,求c.
思路分析:(1)题中已知两边及一边的对角,因此用正弦定理即可;(2)题中是已知两边及其中一边所对的角,但未要求求另一边的对角,则可以用正弦定理也可用余弦定理来求解.
(1)解:由正弦定理,得![]() .
.
所以sinC=![]() .由于c<b,则C必为锐角.
.由于c<b,则C必为锐角.
所以C=30°.
所以A=180°-B-C=180°-45°-30°=105°.
所以![]() .
.
所以a=2sin105°=![]() (或根据余弦定理求a).
(或根据余弦定理求a).
所以S△ABC=![]() acsinB=
acsinB=![]() .
.
(2)解法一:∵![]() ,∴
,∴![]() .
.
又∵b<a,∴B=arcsin![]() ,cosB=
,cosB=![]() .
.
∴sinc=sin(180°-60°-B)=![]() .
.
∴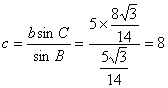 .
.
解法二:因为a2=b2+c2-2bccosA,
所以49=25+c2-10ccos60°.
解得c=8或c=-3(舍去),
所以c=8.
方法归纳 由本题可以看出正弦定理与余弦定理是相通的,结合方程的思想方法,凡是能用正弦定理解的三角形,用余弦定理也能解,反之亦然.在课本中所归结的结论只是一般的求解思路.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014届山西省高二上学期期末理科数学试卷(A)(解析版) 题型:解答题
(本小题满分12分)
如图,在△ABC中, ,
, .
.

(1)求 ;
;
(2)设 的中点为
的中点为 ,求中线
,求中线 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2013届江西省高二下学期第一次月考文科数学 题型:解答题
(本小题满分12分)已知函数 .
.
(1)设 ,且
,且 ,求
,求 的值;
的值;
(2)在△ABC中,AB=1, ,且△ABC面积为
,且△ABC面积为 ,求sinA+sinB的值.
,求sinA+sinB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com