Question

（08年华师一附中二次压轴）过双曲线的右焦点F₂的直线与右支交于A、B两点，且线段AF₂、BF₂的长度分别为m、n，m≥n.

(Ⅰ)求证：mn≥1；

(Ⅱ)当直线AB的斜率k∈[，3]时，求的取值范围.

Answer 1

解析：解法一：(Ⅰ)(1)当直线AB⊥x轴时，则A(，1)，B(，－1)，此时m=n=1，∴mn=1.  

(2)当直线AB不垂直于x轴时，m＞n，设双曲线的右准线为l，作AA₁⊥l于A₁，作BB₁⊥l于B₁，作BK⊥AA₁于K且交x轴于M

根据双曲线第二定义有：|AA₁|=m，|BB₁|=n，而F₂到准线l的距离为.

由=得：=，∴2mn=m+n≥，∴mn≥1，∵此时m≠n，∴mn＞1

综上可知mn≥1

(Ⅱ)设AB：x=ty+，代入双曲线方程得

∴ 

令，则，且y₁=－y₂代入上面两式得：

(1－)y₂=－                          ①

                                ②

消去y₂得即         ③

由k∈[，3]有：，综合③式得3≤+≤4

由＞1得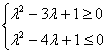

解得∈ 

解法二(Ⅰ)证明：(1)当直线AB斜率不存在时，A(，1)，B(，-1)，∴m=n=1，∴mn=1

(2)当直线AB斜率存在时，设AB：y=k(x－)，A(x₁，y₁)，B(x₂，y₂)

由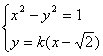得

∵直线AB与双曲线右支有两个交点

∴，∴k²－1＞0

∴mn=|a－ex₁|?|a－ex₂|=(ex₁－a)(ex₂－a)=e²x₁x₂－ae(x₁+x₂)+a²==1+＞1

由(1)(2)知:mn≥1

(Ⅱ)解：由题m＞n，则x₁＞x₂

∵k∈[，3]，∴当直线的斜率k逐渐增大时，y₁减小，|y₂|增大，∴逐渐减小

∴(1)当k=时，－4x²+10x－11=0，∴x_1，2=(x₁＞x₂)，∴此时_max=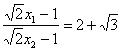 

(2)当k=3时，－8x²+18x－19=0，x_1，2=( x₁＞x₂)，∴此时_min=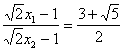

∴的取值范围是