
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源:不详 题型:解答题
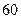 米,宽
米,宽 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米需打建一个桩位,每个桩位需花费
米需打建一个桩位,每个桩位需花费 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 为何值时,所需总费用最少?
为何值时,所需总费用最少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 +
+ =1,求x+y的最小值;
=1,求x+y的最小值; ,求函数y=4x-2+
,求函数y=4x-2+ 的最大值;
的最大值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com