
| a |
| x+1 |
| 9 |
| 2 |
| 1 |
| x |
| ||
| (x+1)2 |
x2+2x+1-
| ||
| x(x+1)2 |
(x-
| ||||
| x(x+1)2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
| ||
| e+1 |
| 9 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |


科目:高中数学 来源: 题型:
| m |
| C |
| 2 |
| n |
| 3 |
| sin2A |
| 1 |
| cos2A |
| 1 |
| cosB |
查看答案和解析>>
科目:高中数学 来源: 题型:
|

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| x |
| a |
| y |
| b |
| ||
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
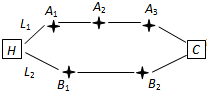 家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为
家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
| 路线 | 距离(公里) | 行驶费用(元/公里) | 遇红灯时 费用(元/次) |
| L1 | 20 | 1.5 | 1.5 |
| L2 | 30 | 1 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com