
设一元二次方程anx2-an+1x+1=0(n=1,2,3,…)有两根α和β,且满足6α-2αβ+6β=3
(1)试用a![]() n表示an+1;
n表示an+1;
(2)求证:数列{an-![]() }是等比数列;
}是等比数列;
(3)当a1=![]() 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.
(1)∵一元二次方程anx2-an+1x+1=0(n=1,2,3,…)有两根α和β,
∴由根与系数的关系易得α+β=![]() ,αβ=
,αβ=![]() ,
,
∵6α-2αβ+6β=3,∴![]() -
-![]() =3,
=3,
即an+1=![]() an+
an+![]() .
.
(2)∵an+1=![]() an+
an+![]() ,∴an+1-
,∴an+1-![]() =
=![]() (an-
(an-![]() ),
),
当an-![]() ≠0时,
≠0时,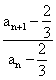 =
=![]() ,
,
当an-![]() =0,即an=
=0,即an=![]() 时,
时,
此时一元二次方程为![]() x2-
x2-![]() x+1=0,
x+1=0,
即2x2-2x+3=0,Δ=4-24<0
∴不合题意,即数列{an-![]() }是等比数列.
}是等比数列.
(3)由(2)知:数列{an-![]() }是以a1-
}是以a1-![]() =
=![]() -
-![]() =
=![]() 为首项,公比为
为首项,公比为![]() 的等比数列,
的等比数列,
∴an-![]() =
=![]() ×(
×(![]() )n-1=(
)n-1=(![]() )n,
)n,
即an=(![]() )n+
)n+![]() ,
,
∴数列{an}的通项公式是an=(![]() )n+
)n+![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
| 5 | 6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 5 |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年安徽省合肥市双凤高中高一(下)期末数学试卷(解析版) 题型:解答题
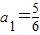 ,且以a1,a2,a3,…,an为系数的一元二次方程an-1x2-anx+1=0(n∈N*,n≥2)都有根α,β,且两个根α,β满足3α-αβ+3β=1.
,且以a1,a2,a3,…,an为系数的一元二次方程an-1x2-anx+1=0(n∈N*,n≥2)都有根α,β,且两个根α,β满足3α-αβ+3β=1.查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆市南开中学高三(上)11月月考数学试卷(理科)(解析版) 题型:解答题
 ,且以a1,a2,a3,…,an为系数的一元二次方程an-1x2-anx+1=0(n∈N*,n≥2)都有根α,β,且两个根α,β满足3α-αβ+3β=1.
,且以a1,a2,a3,…,an为系数的一元二次方程an-1x2-anx+1=0(n∈N*,n≥2)都有根α,β,且两个根α,β满足3α-αβ+3β=1.查看答案和解析>>
科目:高中数学 来源:2011年重庆十一中高考数学一模训练试卷(二)(解析版) 题型:解答题
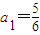 ,且以a1,a2,a3,…,an为系数的一元二次方程an-1x2-anx+1=0(n∈N*,n≥2)都有根α,β,且两个根α,β满足3α-αβ+3β=1.
,且以a1,a2,a3,…,an为系数的一元二次方程an-1x2-anx+1=0(n∈N*,n≥2)都有根α,β,且两个根α,β满足3α-αβ+3β=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com