
设函数![]() 的图象在x=1处取得极值4.
的图象在x=1处取得极值4.
(1)求函数![]() 的单调区问;
的单调区问;
(2)对于函数![]() ,若存在两个不等正数s,t(s<t),当s≤x≤t时,函数y=g(x)的值域是【s,t】,则把区间【s,t】叫函数
,若存在两个不等正数s,t(s<t),当s≤x≤t时,函数y=g(x)的值域是【s,t】,则把区间【s,t】叫函数![]() 的“正保值区间"。问函数
的“正保值区间"。问函数![]() 是否存在,正保值区间",若存在,求出所有的“正保值区间”;若不存在,请说明理由.
是否存在,正保值区间",若存在,求出所有的“正保值区间”;若不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:浙江省衢州市2007年高三年级教学质量检测试卷数学(理科) 题型:044
设函数![]() 的图象在x=1处的切线平行于直线2x―y=0.记g(x)的导函数为f(x).数列{an}满足:
的图象在x=1处的切线平行于直线2x―y=0.记g(x)的导函数为f(x).数列{an}满足:![]() ,an+1=f(an).
,an+1=f(an).
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)试判断数列{an}的增减性,并给出证明;
(Ⅲ)当n≥2,![]() 时,证明:
时,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源:2013届内蒙古赤峰二中、平煤高中高三5月联合考试文科数学试卷(带解析) 题型:填空题
下面6个命题:①把函数 的图象向右平移
的图象向右平移 个单位,得到
个单位,得到 的图象;
的图象;
②函数 的图象在x=1处的切线平行于直线y=x,则
的图象在x=1处的切线平行于直线y=x,则 是f(x)的单调递增区间;
是f(x)的单调递增区间;
③正方体的内切球与其外接球的表面积之比为1∶3;
④“a=2”是“直线ax+2y=0平行于直线x+y=1”的充分不必要条件。
⑤设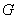 是
是 的重心,且
的重心,且
 ,则角
,则角 的大小为
的大小为 
⑥已知变量 满足约束条件
满足约束条件 ,则
,则 的取值范围是
的取值范围是
其中所有正确命题的序号为________
查看答案和解析>>
科目:高中数学 来源:2012-2013学年内蒙古、平煤高中高三5月联合考试文科数学试卷(解析版) 题型:填空题
下面6个命题:①把函数 的图象向右平移
的图象向右平移 个单位,得到
个单位,得到 的图象;
的图象;
②函数 的图象在x=1处的切线平行于直线y=x,则
的图象在x=1处的切线平行于直线y=x,则 是f(x)的单调递增区间;
是f(x)的单调递增区间;
③正方体的内切球与其外接球的表面积之比为1∶3;
④“a=2”是“直线ax+2y=0平行于直线x+y=1”的充分不必要条件。
⑤设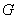 是
是 的重心,且
的重心,且
 ,则角
,则角 的大小为
的大小为 
⑥已知变量 满足约束条件
满足约束条件 ,则
,则 的取值范围是
的取值范围是
其中所有正确命题的序号为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com