Question

已知a，b，c满足：a、b、c∈R⁺，a²+b²=c²，当n∈N，n＞2时，比较cⁿ与aⁿ+bⁿ的大小．

Answer 1

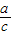
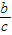
【答案】分析：依题意，a²＜c²，b²＜c²，∈（0，1），∈（0，1），利用指数函数的单调性即可比较n＞2时，cⁿ与aⁿ+bⁿ的大小．
解答：解：∵a、b、c∈R⁺，a²+b²=c²，
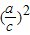
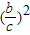
∴+=1．
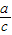
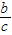
∴∈（0，1），∈（0，1），
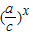
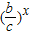
∵y=与y=均为减函数，
∴当n＞2时，＜，＜；
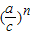
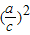
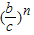
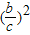
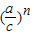
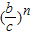
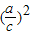
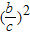
∴当n＞2时，+＜+=1，
即当n＞2时，aⁿ+bⁿ＜cⁿ．
点评：本题考查不等式比较大小，突出考查指数函数的单调性，考查转化思想与推理分析的能力，属于难题．