练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设O为原点，点A、B的坐标分别为(a，0)，(0，a)其中a是正的常数，点P在线段AB上，且＝t(0≤t≤1)，则的最大值为________．

    答案：
    解析：

    a2


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设抛物线y2=8x，O为坐标原点，点A，B是抛物线上的点，
    （1）如果OA、OB的斜率分别为
    12
    ，-2，求直线AB与x轴的交点坐标；
    （2）如果OA⊥OB，求证：直线AB必过定点，并求出定点坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

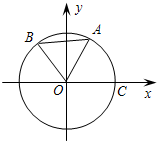    精英家教网如图，O为坐标原点，点A，B，C均在⊙O上，点A(
    3
    5
    ，
    4
    5
    )    ，点B在第二象限，点C（1，0）．
    （Ⅰ）设∠COA=θ，求sin2θ的值；
    （Ⅱ）若△AOB为等边三角形，求点B的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设定义在区间[x1，x2]上的函数y=f（x）的图象为C，点A、B的坐标分别为（x1，f（x1）），（x2f（x2））且M（x，f（x））为图象C上的任意一点，O为坐标原点，当实数λ满足x=λx1+（1-λ）x2时，记向量
    ON
    =λ
    OA
    +(1-λ)
    OB
    ．若|
    MN
    |≤k    恒成立，则称函数y=f（x）在区间[x1，x2]上可在标准k下线性近似，其中k是一个确定的正数．
    （Ⅰ）求证：A、B、N三点共线
    （Ⅱ）设函数f（x）=x2在区间[0，1]上可的标准k下线性近似，求k的取值范围；
    （Ⅲ）求证：函数g（x）=lnx在区间（em，em+1）（m∈R）上可在标准k=
    1
    8
    下线性近似．
    （参考数据：e=2.718，ln（e-1）=0.541）

    查看答案和解析>>

    科目：高中数学 来源：2002年全国各省市高考模拟试题汇编 题型：013

    有四个命题：

    ①若是实数，则正整数n的最小值是4

    ②设z是虚数，则z＋∈

    ③若都是非零复数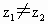，，且复平面上O为原点，点A和B分别与和对应，∠AOB＝，则

    ④若复数z满足|z－|≤1，则≤arg(－zi)≤，其中真命题是

    [　　]

    A．①③④
    B．①②③
    C．①②④
    D．②③④

    查看答案和解析>>

    同步练习册答案