
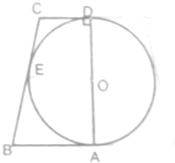
 如图,半圆O的直径为直角梯形垂直于底的腰,且切AB、BC、CD于A、E、D点,将其绕AD所在直线旋转一周,得到一个球与一个圆台,若球的表面积与圆台侧面积的比为3:4,求球的体积与圆台体积之比.
如图,半圆O的直径为直角梯形垂直于底的腰,且切AB、BC、CD于A、E、D点,将其绕AD所在直线旋转一周,得到一个球与一个圆台,若球的表面积与圆台侧面积的比为3:4,求球的体积与圆台体积之比. 分析 设球半径为R,圆台上底半径为r,圆台下底半径为r′,因为球与圆台上下侧面都相切,所以圆台侧面长l=r+r′,结合已知求出r,r′,R之间的关系式,代入球的体积公式和圆台的体积公式,可得答案.
解答 解:设球半径为R,圆台上底半径为r,圆台下底半径为r′,
因为球与圆台上下侧面都相切,所以圆台侧面长l=r+r′,
又∵球面面积与圆台的侧面积之比为3:4,
∴π﹙r+r′﹚2:4πR2=4:3①
﹙r′-r﹚2+﹙2R﹚2=﹙r+r′﹚2②
解之r′=3r,则R=$\sqrt{3}$r,
V球=$\frac{4}{3}$πR3=$\frac{12\sqrt{3}π}{3}$r3,
V台=$\frac{1}{3}$π(r2+r′2+rr′)2R=$\frac{26\sqrt{3}π}{3}$r3,
V球:V台=6:13.
点评 本题考查的知识点是旋转体,熟练掌握圆台和球的表面积公式和体积公式,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | a≥1 | B. | a≥2 | C. | a≤-2 | D. | a<-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{8}{3}$ | C. | $\frac{11}{4}$ | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {2,3} | C. | {1,2,3} | D. | {-1,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com