
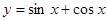 ,②
,②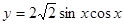 ,则下列结论正确的是
,则下列结论正确的是A.两个函数的图象均关于点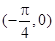 成中心对称 成中心对称 |
B.两个函数的图象均关于直线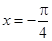 成中心对称 成中心对称 |
C.两个函数在区间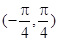 上都是单调递增函数 上都是单调递增函数 |
| D.两个函数的最小正周期相同 |
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源:不详 题型:单选题
 -x)的定义域是 ( )
-x)的定义域是 ( )A.{x|x≠ ,x∈R} ,x∈R} | B.{x|x≠- ,x∈R} ,x∈R} |
C.{x|x≠kπ+ ,k∈Z,x∈R} ,k∈Z,x∈R} | D.{x|x≠kπ+ ,k∈Z,x∈R} ,k∈Z,x∈R} |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
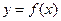 同时具有下列三个性质:(1)最小正周期为
同时具有下列三个性质:(1)最小正周期为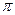 ;(2)图象关于直线
;(2)图象关于直线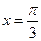 对称;(3)在区间
对称;(3)在区间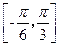 上
上 是增函数,则
是增函数,则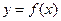 的解析式可以是_______________.
的解析式可以是_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com