若i是虚数单位,则i+2i2+3i3+…+2013i2013= .
【答案】
分析:由虚数单位的周期性可得得i
4n=1,i
4n+1=i,i
4n+2=-1,i
4n+3=-i,其中n为自然数,S=i+2i
2+3i
3+…+2013i
2013,①进而可得:iS=i
2+2i
3+3i
4+…+2013i
2014,②,两式相减,由等比数列的求和公式,结合复数的运算化简即可.
解答:解:由虚数单位i性质可得i
4n=1,i
4n+1=i,i
4n+2=-1,i
4n+3=1,其中n为自然数,
设S=i+2i
2+3i
3+…+2013i
2013,①
两边同乘以i可得:iS=i
2+2i
3+3i
4+…+2013i
2014,②
①-②可得(1-i)S=i+i
2+i
3+…+i
2013-2013i
2014=
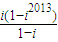
-2013i
2014=
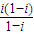
-2013×(-1)=2013+i,
故S=
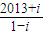
=
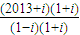
=
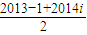
=1006+1007i
故答案为:1006+1007i
点评:本题考查虚数单位及其性质,涉及数列的错位相减法求和以及复数代数形式的加减运算,属中档题.

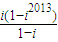 -2013i2014=
-2013i2014=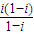 -2013×(-1)=2013+i,
-2013×(-1)=2013+i,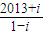 =
=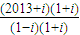 =
=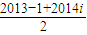 =1006+1007i
=1006+1007i
