
函数f(x)= 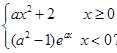 在
在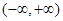 上是单调函数的必要不充分条件是
上是单调函数的必要不充分条件是
A.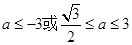 | B. |
C.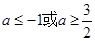 | D.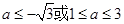 |
D
解析试题分析:由于函数f(x)为分段函数,故要使其为单调增函数,需每段上为增函数且x<0时的最大值小于或等于x≥0时的最小值,同理得出其为单调减函数的条件,因此先求函数为增函数的充要条件,再比较选项中的集合与充要条件集合的包含关系即可判断其充要性.
根据题意函数f(x)= 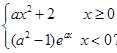 在
在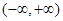 上是单调增函数
上是单调增函数
当x 0时,y=
0时,y= 为二次函数,图象是对称轴为y轴的抛物线,它为增函数时,有a>0;
为二次函数,图象是对称轴为y轴的抛物线,它为增函数时,有a>0;
当x<0时,f(x)=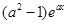 是增函数,它的导函数为f′(x)=a
是增函数,它的导函数为f′(x)=a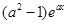 ,
,
令f′(x) 0得-1
0得-1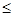 a
a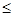 0或a
0或a 1,且
1,且 ≤0即-1
≤0即-1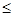 a
a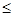 1,
1,
∴综合得a=1;
意函数f(x)= 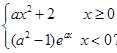 在
在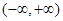 上是单调减函数
上是单调减函数
当x≥0时,y= 为二次函数,图象是对称轴为y轴的抛物线,它为减函数时,有a<0;
为二次函数,图象是对称轴为y轴的抛物线,它为减函数时,有a<0;
当x<0时,f(x)=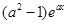 是减函数,它的导函数为f′(x)=a
是减函数,它的导函数为f′(x)=a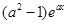 ,
,
令f′(x)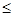 0得
0得
0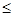 a
a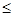 1或a
1或a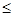 -1,
-1,
且(a2-1)e0 0即a
0即a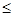 -1或a
-1或a 1,
1,
∴综合得a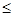 -1.
-1.
综上所述则是单调函数的充要条件是a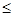 -1或a=1,故那么其必要不充分条件表示的集合要大,故选D.
-1或a=1,故那么其必要不充分条件表示的集合要大,故选D.
考点:分段函数单调性
点评:本题考查了分段函数的单调性的判断方法,判断命题充要性的方法,导函数的应用等,属于基础题.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com