Question

甲、乙两位学生参加数学竞赛培训，现分别从他们的培训期间参加的若干次预赛成中随机抽取8次，记录如下
甲：82，91，79，78，95，88，83，84；乙：92，95，80，75，83，80，90，85．
（1）画出甲、乙两位学生成绩的茎叶图；
（2）现要从中选派一人参加数学竞赛，从统计学角度，你认为派哪位学生参加合请说明理由．
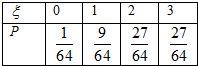
（3）若将频率视为概率，对学生甲在今后的三次数学竞赛成绩进行预测，记这三次成绩中高于80分的次数为ξ，求ξ的分布列及数学期望Eξ．

Answer 1

分析：（1）用茎叶图表示两组数据，首先要先确定“茎”值，再将数据按“茎”值分组分类表示在“叶”的位置．
（2）选派学生参加大型比赛，根据不同的标准选派的方法也不一样①是要寻找成绩优秀的学生，就要分析两名学生的平均成绩②若平均成绩相等，再由茎叶图或是由方差（标准差）分析出成绩相比稳定的学生参加③为了追求高分产生的概率，也可以从高分产生的概率方面对两人进行比较．
（3）数学期望的计算，可先由给定数据列出分布列，再根据数学期望的计算公式给出结果．

解答：解：（1）茎叶图如图


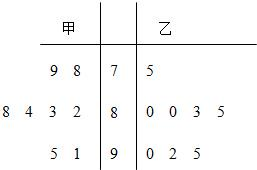
（2）方法一：（根据成绩稳定的优秀学生参加原则）

.

x甲

=

.

x乙

=85，但S_甲²＜S_乙²
所以选派甲合适（6分）
方法二：（根据高分产生概率高的学生参加原则）
假设含9（0分）为高分，则甲的高分率为

2

8

，乙的高分率为

3

8

，
所以派乙合适．
或：假设含8（5分）为高分，则甲的高分率为

3

8

，乙的高分率为

1

2

，
所以派乙合适．
（3）甲高于8（0分）的频率为

6

8

=

3

4

（7分）ξ的可能取值为0、1、2、3
∵ξ～B(3，

3

4

)，
∴P(ξ=k)=

C

k 3

(

3

4

)k(

1

4

)3-k，（k=0，1，2，3）
∴ξ的分布列为

∴Eξ=3×

3

4

=

9

4

（12分）

点评：根据新高考服务于新教材的原则，作为新教材的新增内容--“茎叶”图是新高考的重要考点，同时（2）中概率、数学期望的计算也是高考的热点．对于“茎叶图”学习的关键是学会画图、看图和用图，对于概率要多练习使用列举法表示满足条件的基本事件个数．对于数学期望的计算则要熟练掌握运算方法和步骤．