
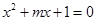 有两个不等的负根;
有两个不等的负根;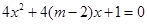 无实根.若“p或q”为真,“p且q”为假,
无实根.若“p或q”为真,“p且q”为假,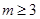 ;(2)
;(2)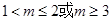 。
。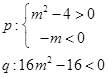 ----------------4分
----------------4分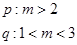 --------------6分
--------------6分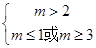 得
得 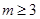 -----------------9分
-----------------9分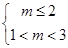 得
得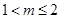 --------------11分
--------------11分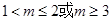 ---------12分
---------12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com