
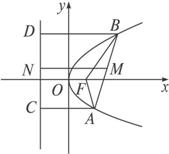
解:如图,设F是抛物线y2=x的焦点,A、B两点到准线的垂线分别是AC、BD,M点到准线的垂线为MN,N为垂足,则|MN|=![]() (|AC|+|BD|),
(|AC|+|BD|),
根据抛物线定义得:|AC|=|AF|,|BD|=|BF|,
∴|MN|=![]() (|AF|+|BF|)≥
(|AF|+|BF|)≥![]() .
.
设M点的横坐标为x,则:|MN|=x+![]() .∴x=|MN|-
.∴x=|MN|-![]() ≥
≥![]() -
-![]() =
=![]() .
.
等号成立的条件是弦AB过点F,由于|AB|>2p=1,
∴AB过焦点是可能的,此时M点到y轴最短距离是![]() ,即AB的中点横坐标为
,即AB的中点横坐标为![]() .当F在AB上时,设A、B的纵坐标分别为y1、y2,则y1y2=-p2=-
.当F在AB上时,设A、B的纵坐标分别为y1、y2,则y1y2=-p2=-![]() ,从而(y1+y2)2=y12+y22+2y1y2=2×
,从而(y1+y2)2=y12+y22+2y1y2=2×![]() -
-![]() =2.
=2.
∴y1+y2=±![]() ,∴此时AB中点的纵坐标为±
,∴此时AB中点的纵坐标为±![]() ,
,
∴M的坐标为(![]() ,±
,±![]() )时,M到y轴距离的最小值为
)时,M到y轴距离的最小值为![]() .
.
点拨:此题的难点是求最小值.而利用抛物线定义及梯形中位线性质等几何知识使问题变得非常简单,这再一次说明在解题中注意运用圆锥曲线的定义及有关的几何知识,对解题是非常有益的.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2010-2011学年湖北省孝感高中高二(上)期中数学试卷(文科)(解析版) 题型:解答题
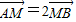 .
.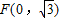 且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省武汉二中、龙泉中学联考高二(下)期末数学试卷(理科)(解析版) 题型:解答题
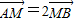 .
.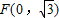 且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com