
已知奇函数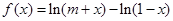
(1)试确定 的值;
的值;
(2)若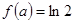 ,求
,求 的值;
的值;
(3)求函数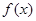 在
在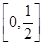 上的最小值.
上的最小值.
(1)因为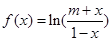 是奇函数
是奇函数
∴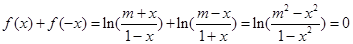
∴ 即
即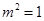 ,
, ------------------------------------------3分
------------------------------------------3分
当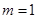 时,
时,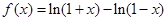 ,由
,由 可得定义域为(-1,1),符合题意;
可得定义域为(-1,1),符合题意;
当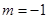 时,
时,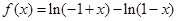 ,
, 无解,舍去.
无解,舍去.
综上,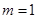 .---------------------------------------------------------------------------4分
.---------------------------------------------------------------------------4分
(2)由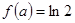 ,知
,知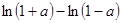
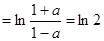
得  解得
解得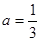
满足 ,所以
,所以 的值为
的值为 ----------7分
----------7分
(3)
设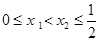 ,则
,则
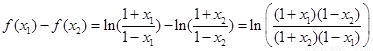
∵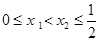 ∴
∴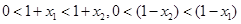
∴ ∴
∴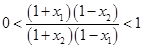
∴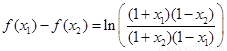
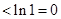
∴函数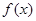 在
在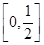 上为增函数-------------------------------------------------------------------10分
上为增函数-------------------------------------------------------------------10分
∴函数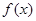 在
在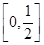 上有最小值
上有最小值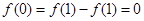
【解析】略


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
已知函数![]() 的图象经过点A(0,1),B
的图象经过点A(0,1),B![]() ,且当
,且当![]() 时,
时,![]()
![]()
![]() 取最大值
取最大值![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)是否存在向量![]() ,使得将
,使得将![]() 的图象按向量
的图象按向量![]() 平移后可以得到一个奇函数的图象?若存在,求出满足条件的一个
平移后可以得到一个奇函数的图象?若存在,求出满足条件的一个![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省中山市高三第二次月考数学理卷 题型:解答题
14分)
(1)已知 是奇函数,求常数m的值;
是奇函数,求常数m的值;
(2)画出函数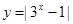 的图象,并利用图象回答:
的图象,并利用图象回答:
k为何值时,方程|3x-1|=k无解?有一解?有两解?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com