
| A. | $\sqrt{2}$f($\frac{π}{4}$)<f($\frac{π}{3}$) | B. | $\sqrt{3}$f($\frac{π}{6}$)<f($\frac{π}{3}$) | C. | cos1•f(1)>$\frac{\sqrt{3}}{2}$f($\frac{π}{6}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)<$\sqrt{3}$f($\frac{π}{6}$) |
分析 根据条件构造函数g(x),求函数的导数,利用函数的单调性即得到结论.
解答 解:因为x∈(0,$\frac{π}{2}$),所以sinx>0,cosx>0,
由tanx•f(x)>f′(x),得f′(x)cosx<f(x)sinx,
即f′(x)cosx-f(x)sinx<0.
令g(x)=cosxf(x),x∈(0,$\frac{π}{2}$),
则g′(x)=f′(x)cosx-f(x)sinx<0,
所以函数g(x)在x∈(0,$\frac{π}{2}$)上为减函数,
则g($\frac{π}{6}$)>g($\frac{π}{4}$)>g(1)>g($\frac{π}{3}$),
则cos($\frac{π}{6}$)f($\frac{π}{6}$)>cos($\frac{π}{4}$)f($\frac{π}{4}$)>cos(1)f(1)>cos($\frac{π}{3}$)f($\frac{π}{3}$),
∴$\sqrt{3}$f($\frac{π}{6}$)>$\sqrt{2}$f($\frac{π}{4}$)>2cos(1)f(1)>f($\frac{π}{3}$),
故D正确,A,B,C错误,
故选:D.
点评 本题考查了导数的运算法则,考查了利用函数导函数的符号判断函数的单调性,考查了函数构造法,属中档题型


科目:高中数学 来源: 题型:解答题
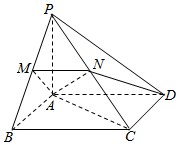 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC上的点,MN⊥PB.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC上的点,MN⊥PB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
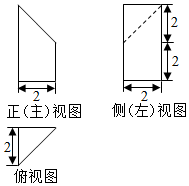
| A. | $\frac{10}{3}$ | B. | 4 | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{9}{4}$,+∞) | B. | [2,+∞) | C. | (-∞,$\frac{9}{4}$] | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 24 | C. | 36 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{10}}{4}$ | D. | $\frac{\sqrt{10}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com