
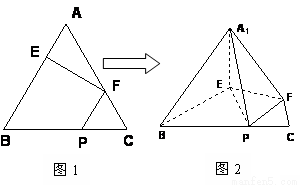
(本题满分8分)在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到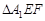 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求二面角A1-BP-E的大小。
(Ⅰ)证明略
(Ⅱ)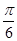
【解析】不妨设正三角形的边长为3,则
(I)在图1中,取BE的中点D,连结DF,
∵AE∶EB=CF∶FA=1∶2,∴AF=AD=2,而∠A=60o,∴△ADF为正三角形。
又AE=DE=1,∴EF⊥AD。
在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的一个平面角,
由题设条件知此二面角为直二面角,∴A1E⊥BE。
又BE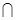 EF=E,∴A1E⊥面BEF,即A1E⊥面BEP。
EF=E,∴A1E⊥面BEF,即A1E⊥面BEP。
(II)在图2中,过E点作BP的垂线,并交BP于G点,连接A1G,由(I)知A1E⊥平面BEP,∴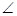 A1GE即为二面角A1-BP-E的平面角,又A1E=1,GE=
A1GE即为二面角A1-BP-E的平面角,又A1E=1,GE=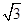 ,∴
,∴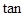
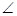 A1GE=
A1GE=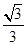 ,∴
,∴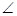 A1GE=
A1GE=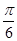 ,即所求为
,即所求为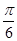 。
。


科目:高中数学 来源: 题型:
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
在数列![]() 中,
中,![]() ,
,![]() .
.
(1)设![]()
![]() ,证明:数列
,证明:数列![]() 是等差数列;
是等差数列;
(2)设![]() 数列
数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,是否存在
,是否存在![]() 实数
实数![]() ,使得对任意的正整数
,使得对任意的正整数![]() 和实数
和实数![]() ,都有
,都有![]() 成立?请说明理由.
成立?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市长宁区高三教学质量测试理科数学 题型:解答题
(本题满分12分)本题共有2个小题,第1小题满分8分,第2小题满分4分.
在正四棱柱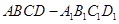 中,已知底面
中,已知底面 的边长为2,点P是
的边长为2,点P是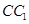 的中点,直线AP与平面
的中点,直线AP与平面 成
成 角.
角.
(文)(1)求 的长;
的长;
(2)求异面直线 和AP所成角的大小.(结果用
和AP所成角的大小.(结果用
反三角函数值表示);
(理)(1)求异面直线 和AP所成角的大小.(结果用
和AP所成角的大小.(结果用
反三角函数值表示) ;
(2)求点 到平面
到平面 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源:上海市闵行区2010届高三第二次模拟考试数学文 题型:解答题
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
在数列 中,
中,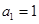 ,
, .
.
(1)设
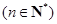 ,证明:数列
,证明:数列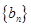 是等差数列;
是等差数列;
(2)设数列 的前
的前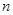 项和为
项和为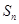 ,求
,求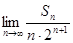 的值;
的值;
(3)设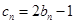 ,数列
,数列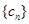 的前
的前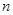 项和为
项和为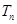 ,
,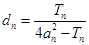 ,是否存在实数
,是否存在实数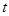 ,使得对任意的正整数
,使得对任意的正整数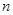 和实数
和实数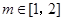 ,都有
,都有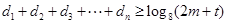 成立?请说明理由.
成立?请说明理由.
查看答案和解析>>
科目:高中数学 来源:上海市闵行区2010届高三第二次模拟考试数学文 题型:解答题
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
在数列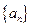 中,
中, ,
,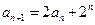 .
.
(1)设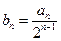
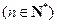 ,证明:数列
,证明:数列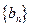 是等差数列;
是等差数列;
(2)设 数列
数列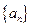 的前
的前 项和为
项和为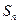 ,求
,求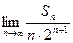 的值;
的值;
(3)设 ,数列
,数列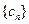 的前
的前 项和为
项和为 ,
,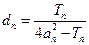 ,是否存在
,是否存在 实数
实数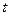 ,使得对任意的正整数
,使得对任意的正整数 和实数
和实数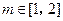 ,都有
,都有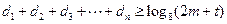 成立?请说明理由.
成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com