
如图,正四棱锥S-ABCD的底面是边长为a正方形,O为底面对角线交点,侧棱长是底面边长的![]() 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.
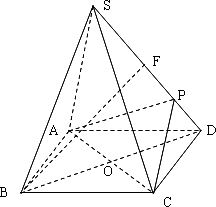
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,F为SD中点,求证:BF∥平面PAC;
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE:EC的值;若不存在,试说明理由.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
 如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°.
如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°.查看答案和解析>>
科目:高中数学 来源: 题型:
 12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( )
12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( )查看答案和解析>>
科目:高中数学 来源: 题型:
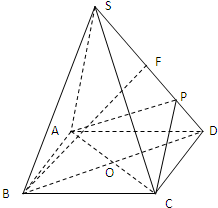 如图,正四棱锥S-ABCD 的底面是边长为a正方形,O为底面对角线交点,侧棱长是底面边长的
如图,正四棱锥S-ABCD 的底面是边长为a正方形,O为底面对角线交点,侧棱长是底面边长的| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2006•西城区二模)如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的
(2006•西城区二模)如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com