分析:(Ⅰ)连接OC,先根据△AOC是等腰直角三角形证出中线OD⊥AC,再结合PO⊥AC证出AC⊥POD,利用平面与平面垂直的判定定理,可证出平面POD⊥平面PAC;
(Ⅱ)过O分别作OH⊥PD于H,OG⊥PA于G,再连接GH,根据三垂线定理证明∠OGH为二面角B-PA-C的平面角,最后分别在Rt△ODA、Rt△ODP、Rt△OGH中计算出OH、OG和sin∠OGH,最后求出所求二面角的余弦值.
解答:
解:(Ⅰ)连接OC,
∵OA=OC,D是AC的中点
∴AC⊥OD
又∵PO⊥底面⊙O,AC?底面⊙O
∴AC⊥PO
∵OD、PO是平面POD内的两条相交直线
∴AC⊥平面POD,
而AC?平面PAC
∴平面POD⊥平面PAC
(Ⅱ)在平面POD中,过O作OH⊥PD于H,由(Ⅰ)知,平面POD⊥平面PAC
所以OH⊥平面PAC,
又∵PA?平面PAC
∴PA⊥HO
在平面PAO中,过O作OG⊥PA于G,连接GH,则有PA⊥平面OGH,从而PA⊥HG.故∠OGH为二面角B-PA-C的平面角
在Rt△ODA中,OD=OA•sin45°=
在Rt△ODP中,OH=
==在Rt△OPA中,OG=
==在Rt△OGH中,sin∠OGH=
==所以cos∠OGH=
==故二面角B-PA-C的余弦值为
点评:直线与平面垂直是证明空间垂直的关键,立体几何常常利用三垂线定理作辅助线,来求与二面角的平面角有关的问题.

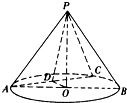 如图,在圆锥PO中,已知PO=
如图,在圆锥PO中,已知PO=
 解:(Ⅰ)连接OC,
解:(Ⅰ)连接OC,

 如图,在圆锥PO中,已知PO=
如图,在圆锥PO中,已知PO=
 ,⊙OD的直径AB=2,点C在
,⊙OD的直径AB=2,点C在 上,且∠CAB=30°,D为AC的中点.
上,且∠CAB=30°,D为AC的中点.
 如图,在圆锥PO中,已知PO=
如图,在圆锥PO中,已知PO= ,⊙O的直径AB=2,C是
,⊙O的直径AB=2,C是 的中点,D为AC的中点.
的中点,D为AC的中点. 如图,在圆锥PO中,已知PO=
如图,在圆锥PO中,已知PO= ,⊙OD的直径AB=2,点C在
,⊙OD的直径AB=2,点C在 上,且∠CAB=30°,D为AC的中点.
上,且∠CAB=30°,D为AC的中点.