已知a为实数,f(x)=(x2-4)(x-a),f′(x)为f(x)的导函数.
(Ⅰ)若f′(-1)=0,求f(x)在[-2,2]上的最大值和最小值;
(Ⅱ)若f(x)在(-∞,-2]和[2,+∞)上均单调递增,求a的取值范围.
【答案】
分析:(I)结合已知中函数的解析式及f′(-1)=0,构造方程求出a值,进而分析出函数的单调性后,求出函数的极值和端点对应的函数值,比照后可得答案.
(II)若f(x)在(-∞,-2]和[2,+∞)上均单调递增,则f′(x)=3x
2-2ax-4≥0对(-∞,-2]恒成立且f′(x)=3x
2-2ax-4≥0对[2,+∞)恒成立,解不等式组可得答案.
解答:解:(I)∵f(x)=(x
2-4)(x-a),
∴f′(x)=2x(x-a)+(x
2-4)
又∵f′(-1)=-2×(-1-a)+(1-4)=0,
∴a=

∴f(x)=(x
2-4)(x-

),
∴f′(x)=2x(x-

)+(x
2-4)=3x
2-x-4
令f′(x)=0,
解得x=-1,x=

,
当x∈[-2,-1]时,f′(x)≤0恒成立,f(x)为减函数
当x∈[-1,4/3]时,f′(x)≥0恒成立,f(x)为增函数,
当x∈[4/3,2]时,f′(x)≤0恒成立,f(x)为减函数
又∵f(-2)=0,f(-1)=

,f(

)=-
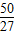
,f(2)=0
可以得到最大值为

,最小值为-
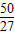
(II)∵f(x)=(x
2-4)(x-a),
∴f′(x)=3x
2-2ax-4,
依题意:f′(x)=3x
2-2ax-4≥0对(-∞,-2]恒成立,即
2ax≤3x
2-4
∴a≥

又∵y=
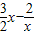
在(-∞,-2]上为增函数,故x=-2时,

取最大值-2,
所以a≥-2
f′(x)=3x
2-2ax-4≥0对[2,+∞)恒成立,即
2ax≤3x
2-4
∴a≤

又∵y=
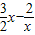
在[2,+∞)上为增函数,故x=2时,
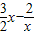
取最小值2,
所以a≤2
故a的取值范围为[-2,2].
点评:本题考查的知识点是利用导数求闭区间上函数的最值,利用导数研究函数的单调性,是导数的综合应用,难度较大.


 ),
), )+(x2-4)=3x2-x-4
)+(x2-4)=3x2-x-4 ,
, ,f(
,f( )=-
)=-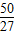 ,f(2)=0
,f(2)=0 ,最小值为-
,最小值为-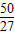

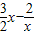 在(-∞,-2]上为增函数,故x=-2时,
在(-∞,-2]上为增函数,故x=-2时, 取最大值-2,
取最大值-2,
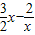 在[2,+∞)上为增函数,故x=2时,
在[2,+∞)上为增函数,故x=2时,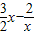 取最小值2,
取最小值2,

 阅读快车系列答案
阅读快车系列答案