
有一段“三段论”,推理是这样的:对于可导函数 ,如果
,如果 ,那么
,那么 是函数
是函数 的极值点,因为
的极值点,因为 在
在 处的导数值
处的导数值 ,所以
,所以 是函数
是函数 的极值点.以上推理中( )
的极值点.以上推理中( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.结论正确
A
【解析】
试题分析:在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是推理形式错误,我们分析的其大前提的形式:“对于可导函数f(x),如果f'(x0)=0,那么x=x0是函数f(x)的极值点”,不难得到结论.解:∵大前提是:“对于可导函数f(x),如果f'(x0)=0,那么x=x0是函数f(x)的极值点”,不是真命题,因为对于可导函数f(x),如果f'(x0)=0,且满足当x>x0时和当x<x0时的导函数值异号时,那么x=x0是函数f(x)的极值点,∴大前提错误故选A
考点:演绎推理
点评:本题考查的知识点是演绎推理的基本方法,演绎推理是一种必然性推理,演绎推理的前提与结论之间有蕴涵关系.因而,只要前提是真实的,推理的形式是正确的,那么结论必定是真实的,但错误的前提可能导致错误的结论


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省北仑中学高二(2-6班)下期中考试数学卷(带解析) 题型:单选题
有一段“三段论”,推理是这样的:对于可导函数 ,如果
,如果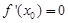 ,那么
,那么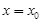 是函数
是函数 的极值点,因为
的极值点,因为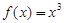 在
在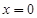 处的导数值
处的导数值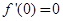 ,所以
,所以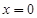 是函数
是函数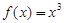 的极值点.以上推理中( )
的极值点.以上推理中( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
查看答案和解析>>
科目:高中数学 来源:黑龙江省哈尔滨市2010届高二下学期期中考试(文科) 题型:选择题
有一段“三段论”推理是这样的:
对于可导函数 ,如果
,如果 ,那么
,那么 是函数
是函数 的极值点,因为函数
的极值点,因为函数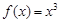 在
在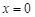 处的导数值
处的导数值 ,所以
,所以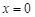 是函数
是函数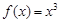 的极值点.以上推理中 ( )
的极值点.以上推理中 ( )
A.大前提错误 B. 小前提错误 C.推理形式错误 D.结论正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com