
已知函数![]() (
(![]() >0),过点P(1,0)作曲线
>0),过点P(1,0)作曲线![]() 的两条切线PM、PN,为M、N.
的两条切线PM、PN,为M、N.
(1)当t=2时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设|MN|=g(t),求函数g(t)的表达式;
(3)在(2)的条件下,若对任意正整数![]() ,在区间[2,
,在区间[2,![]() +
+![]() ]内总存在
]内总存在![]() +1个实数
+1个实数![]() 、
、![]() 、…、
、…、![]() 、
、![]() ,使得不等式g(
,使得不等式g(![]() )+g(
)+g(![]() )+…+g(
)+…+g(![]() )<g(
)<g(![]() )成立,求
)成立,求![]() 的最大值.
的最大值.
解:(1)当t=2时,![]() ,
,
![]()
解得![]() >
>![]() 或
或![]() <一
<一![]() .
.
则函数![]() 的单调递增区间为(一∞,一
的单调递增区间为(一∞,一![]() ),(
),(![]() ,+∞).
,+∞).
(2)设M、N两点的横坐标分别为![]() 1、
1、![]() 2,
2,
∵![]() ,
,
∴切线PM的方程为![]() ,
,
又∵切线PM过点P(1,0),
∴有0一(![]() )=(
)=(![]() ) (1-
) (1-![]() ).
).
即![]() ①
①
同理,由切线PN也过点P(1,0),得
![]() ②
②
由①②可得![]() 1、
1、![]() 2是方程
2是方程![]() =0的两个根,
=0的两个根,
∴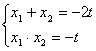 (*)
(*)
|MN|=
=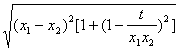
=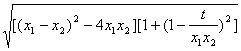
把(*)式代入,得|MN|=![]() ,
,
因此,函数g(*)的表达式为g(t)= ![]() (t>0).
(t>0).
(3)易知g(t)在区间[2,![]() +
+![]() ]上为增函数,
]上为增函数,
∴g(2)≤g(![]() )(
)(![]() =1,2,…,m+1),
=1,2,…,m+1),
则m?g(2)≤g(![]() 1)+g(
1)+g(![]() 2)+…+g(
2)+…+g(![]() m),
m),
∵g(![]() 1)+g(
1)+g(![]() 2)+…+g(
2)+…+g(![]() m)≤g(
m)≤g(![]() m+1)对一切正整数
m+1)对一切正整数![]() 成立.
成立.
∴不等式m?g(2)≤g(![]() +
+![]() )对一切的正整数
)对一切的正整数![]() 恒成立.
恒成立.
∴![]() .
.
即m<![]() 对一切正整数,
对一切正整数,![]() 恒成立.
恒成立.
∵![]() +64≥16.
+64≥16.
∴![]()
>![]() .
.
M<![]() .
.
由于m为正整数,∴m≤6.
又m=6时,存在![]() 1=
1=![]() 2=…=
2=…=![]() m=2,
m=2,![]() m十1=16,
m十1=16,
对所有的![]() 满足条件.因此,m的最大值为6.
满足条件.因此,m的最大值为6.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源:2011-2012学年广东省山一中高三热身练理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数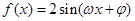 (
(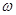 >0,0<
>0,0<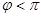 )的最小正周期为
)的最小正周期为 ,且
,且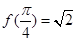 .
.
(1)求 的值;
的值;
(2)若
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com