
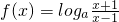 ,(a>0,且a≠1)
,(a>0,且a≠1)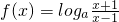 在定义域上是奇函数;
在定义域上是奇函数; 恒成立,求m的取值范围;
恒成立,求m的取值范围; ,解得x<-1或x>1,∴函数的定义域为(-∞,-1)∪(1,+∞).
,解得x<-1或x>1,∴函数的定义域为(-∞,-1)∪(1,+∞).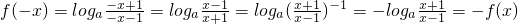
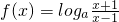 在定义域上是奇函数.
在定义域上是奇函数. 恒成立,
恒成立,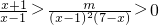 对x∈[2,4]恒成立,
对x∈[2,4]恒成立,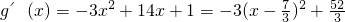 ,
, 恒成立,
恒成立,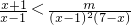 对x∈[2,4]恒成立,∴m>(x+1)(x-1)(7-x)在x∈[2,4]恒成立.
对x∈[2,4]恒成立,∴m>(x+1)(x-1)(7-x)在x∈[2,4]恒成立.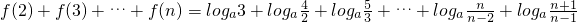 =
=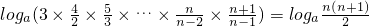 ,∴
,∴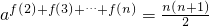
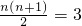 ,2n-2=2,∴af(2)+f(3)+…+f(n)>2n-2,
,2n-2=2,∴af(2)+f(3)+…+f(n)>2n-2, ,2n-2=6,∴af(2)+f(3)+…+f(n)=2n-2,
,2n-2=6,∴af(2)+f(3)+…+f(n)=2n-2,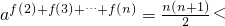 2n-2,下面证明:当n≥4时,
2n-2,下面证明:当n≥4时,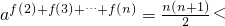 2n-2.
2n-2. ,
,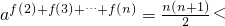 2n-2.
2n-2.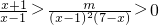 对x∈[2,4]恒成立,即0<m<(x+1)(x-1)(7-x)
对x∈[2,4]恒成立,即0<m<(x+1)(x-1)(7-x) 得到证明.
得到证明.

科目:高中数学 来源:2010-2011学年湖北省武汉市武昌区高一(下)期末数学试卷(解析版) 题型:解答题
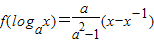 ,其中a>0且a≠1.
,其中a>0且a≠1.查看答案和解析>>
科目:高中数学 来源:2013年北京市西城区高考数学二模试卷(文科)(解析版) 题型:解答题
 ,其中a>0.
,其中a>0.查看答案和解析>>
科目:高中数学 来源:2010年湖北省实验中学高考最后冲刺数学试卷(理科)(解析版) 题型:选择题
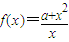 ,(a>0),x∈(0,b),则下列判断正确的是( )
,(a>0),x∈(0,b),则下列判断正确的是( )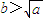 时,f(x)的最小值为
时,f(x)的最小值为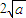
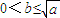 时,f(x)的最小值为
时,f(x)的最小值为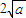
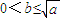 时,f(x)的最小值为
时,f(x)的最小值为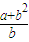
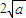
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省豫南九校高三第一次联考数学试卷(理科)(解析版) 题型:解答题
 +bx(a>0)且f′(1)=0,
+bx(a>0)且f′(1)=0,查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省烟台市高三年级期末考试文科数学 题型:选择题
已知函数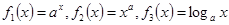 (其中a>0,且a≠),在同一坐标系中画出其中两个函数在第一象限内的图像,其中正确的是
(其中a>0,且a≠),在同一坐标系中画出其中两个函数在第一象限内的图像,其中正确的是

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com