
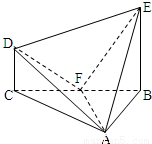
(本题13分)在几何体ABCDE中,∠BAC= 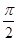 ,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.
(1)求证:DC∥平面ABE;
(2)求证:AF⊥平面BCDE;
(3)求几何体ABCDE的体积.
(1)证明:见解析;(2)证明:见解析;(3)2。
【解析】本题考查线面平行,考查线面垂直,考查几何体的体积,解题的关键是正确线面平行、垂直的判定方法,正确运用体积公式.
(I)证明DC∥平面ABE,即证DC∥EB,利用DC⊥平面ABC,EB⊥平面ABC可证;
(II)证明AF⊥平面BCDE,利用线面垂直的判定,证明DC⊥AF,AF⊥BC即可;
(III)几何体ABCDE的体积就是以平面BCDE为底面,AF为高的三棱锥的体积.
(1)证明:
∵DC⊥平面ABC,EB⊥平面ABC,∴DC∥EB,
又∵DC⊄平面ABE,EB⊂平面ABE,
∴DC∥平面ABE
(2)证明:∵DC⊥平面ABC,AF⊂平面ABC
∴DC⊥AF,又∵AB=AC,F是BC的中点,∴AF⊥BC,
又∵DC∩BC=C,DC⊂平面BCDE,BC⊂平面BCDE,
∴AF⊥平面BCDE
(3)解:∵DC⊥平面ABC,EB⊥平面ABC,
∴DC∥EB,且四边形BCDE为直角梯形
∵在△ABC中,∠BAC=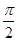 ,AB=AC=2,F是BC的中点
,AB=AC=2,F是BC的中点
∴BC=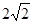 ,AF=
,AF=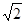
∵由(II)可知AF⊥平面BCDE
∴几何体ABCDE的体积就是以平面BCDE为底面,AF为高的三棱锥的体积
∴VABCDE=VA-BCDE=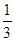 SBCDE×AF=
SBCDE×AF=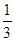 ×
×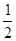 (1+2)×
(1+2)×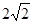 ×
×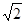 =2
=2


科目:高中数学 来源:2011届陕西省师大附中、西工大附中高三第七次联考理数 题型:解答题
(本题12分)在几何体 中,
中, 是等腰直角三角形,
是等腰直角三角形,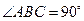 ,
, 和
和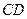 都垂直于平面
都垂直于平面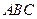 ,且
,且 ,点
,点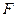 是
是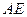 的中点。
的中点。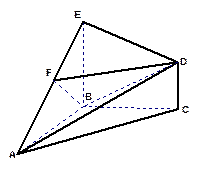
(1)求证: 平面
平面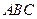 ;
;
(2)求面 与面
与面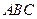 所成的角余弦值
所成的角余弦值 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题13分)在2007全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩;
(2)分别计算两个样本的平均数![]() 和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。
和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com