练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    对任意的实数x，有x3=a0+a1（x-2）+a2（x-2）2+a3（x-2）3，则a2的值是        。
    6
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知二次函数f（x）=ax2+bx+c（a、b、c∈R），且同时满足：①f（-1）=0；②对任意的实数x恒有x≤f（x）≤（
    x+12
    ） 2成立．
    （1）求f（1）；
    （2）求f（x）的表达式；
    （3）当x∈[-1，1]时，函数g（x）=f（x）-mx（m是实数）是单调函数，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    有下列四个命题:

    ①22 340能被3或5整除；②不存在x∈R,使得x2+x+1＜0；③对任意的实数x,均有x+1＞x；④方程x2-2x+3=0有两个不等的实根.

    其中假命题有___________________.（只填序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    有下列四个命题:①22 340能被3或5整除；②不存在x∈R,使得x2+x+1＜0；③对任意的实数x,均有x+1＞x；④方程x2-2x+3=0有两个不等的实根.其中假命题有__________(只填序号).

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年吉林省吉林一中高三（上）第三次月考数学试卷（文科）（解析版） 题型：选择题

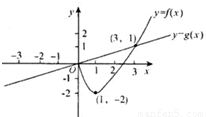
    对任意的实数a、b，记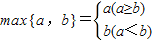．若F（x）=max{f（x），g（x）}（x∈R），其中奇函数y=f（x）在x=l时有极小值-2，y=g（x）是正比例函数，函数y=f（x）（x≥0）与函数y=g（x）的图象如图所示．则下列关于函数y=F（x）的说法中，正确的是（ ）
    A．y=F（x）为奇函数
    B．y=F（x）有极大值F（-1）且有极小值F（0）
    C．y=F（x）在（-3，0）上为增函数
    D．y=F（x）的最小值为-2且最大值为2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    有下列四个命题:

    ①22340能被3或5整除;②不存在x∈R,使得x2+x+1＜0;③对任意的实数x,均有x+1＞x;④方程x2-2x+3=0有两个不等的实根.其中假命题有______.(只填序号)

    查看答案和解析>>

    同步练习册答案