
分析 数列{an-4}是公比为-$\frac{1}{2}$的等比数列,可得an=4+$(-\frac{1}{2})^{n-1}$,利用求和公式可得:数列{an}的前n项和Sn=4n+$\frac{2}{3}$$[1-(-\frac{1}{2})^{n}]$,由于对于任意n∈N*,都有P(Sn-4n)∈[1,3],可得$\frac{1}{1-(-\frac{1}{2})^{n}}$≤$\frac{2p}{3}$≤$\frac{3}{1-(-\frac{1}{2})^{n}}$.对n分类讨论,利用数列的单调性与不等式的性质即可得出.
解答 解:∵数列{an-4}是公比为-$\frac{1}{2}$的等比数列,∴an-4=(a1-4)×$(-\frac{1}{2})^{n-1}$,a1=5,
∴an=4+$(-\frac{1}{2})^{n-1}$,
∴数列{an}的前n项和Sn=4n+$\frac{1-(-\frac{1}{2})^{n}}{1-(-\frac{1}{2})}$=4n+$\frac{2}{3}$$[1-(-\frac{1}{2})^{n}]$,
∴Sn-4n=$\frac{2}{3}$$[1-(-\frac{1}{2})^{n}]$,
由于对于任意n∈N*,都有P(Sn-4n)∈[1,3],
∴$\frac{1}{1-(-\frac{1}{2})^{n}}$≤$\frac{2p}{3}$≤$\frac{3}{1-(-\frac{1}{2})^{n}}$.
∴
n为奇数时,$\frac{1}{1-(-\frac{1}{2})^{n}}$∈$[\frac{2}{3},1)$;
n为偶数时,$\frac{1}{1-(-\frac{1}{2})^{n}}$∈$(1,\frac{4}{3}]$.
∴$\frac{4}{3}$≤$\frac{2p}{3}$≤2,解得2≤p≤3.
则实数P的取值范围是[2,3].
故答案为:[2,3].
点评 本题考查了等差数列的通项公式与求和公式、数列的单调性、不等式的性质,考查了分类讨论方法、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=x+1,$g(x)=\frac{{x({x+1})}}{x}$ | B. | f(x)=1,$g(x)=\frac{x}{|x|}$ | C. | y=|x|,$y=\sqrt{x^2}$ | D. | $f(x)=\sqrt{x^2}+1$,g(x)=x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
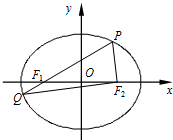 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设$\overrightarrow{P{F}_{1}}$=λ$\overrightarrow{{F}_{1}Q}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设$\overrightarrow{P{F}_{1}}$=λ$\overrightarrow{{F}_{1}Q}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -1 | C. | 0 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3<x<2 | B. | -2<x<3 | C. | -5<x<1 | D. | -1<x<5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com