
【题目】已知函数![]() ,
,![]() 的在数集
的在数集![]() 上都有定义,对于任意的
上都有定义,对于任意的![]() ,当
,当![]() 时,
时,![]() 或
或![]() 成立,则称
成立,则称![]() 是数集
是数集![]() 上
上![]() 的限制函数.
的限制函数.
(1)求![]() 在
在![]() 上的限制函数
上的限制函数![]() 的解析式;
的解析式;
(2)证明:如果![]() 在区间
在区间![]() 上恒为正值,则
上恒为正值,则![]() 在
在![]() 上是增函数;[注:如果
上是增函数;[注:如果![]() 在区间
在区间![]() 上恒为负值,则
上恒为负值,则![]() 在区间
在区间![]() 上是减函数,此结论无需证明,可以直接应用]
上是减函数,此结论无需证明,可以直接应用]
(3)利用(2)的结论,求函数![]() 在
在![]() 上的单调区间.
上的单调区间.
【答案】(1)![]() ;(2)证明见解析;(3)见解析.
;(2)证明见解析;(3)见解析.
【解析】
(1)由题目给出的条件,构造![]() ,根据条件验证可得所求函数;
,根据条件验证可得所求函数;
(2)运用反证法,即可得证;
(3)求得![]() ,根据第二问结论由
,根据第二问结论由![]() 大于0,可得增区间;
大于0,可得增区间;![]() 小于0,可得减区间.
小于0,可得减区间.
解:(1)任意的![]() ,
,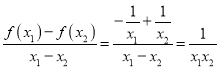 ;
;
由于任意性:![]() ;
;
故构造![]() ;
;
由幂函数性质得![]() 在
在![]() 单调递减,
单调递减,
且易得:![]()
![]() ,满足题意,
,满足题意,
故:![]() ;
;
(2)运用反证法,即假设![]() 在
在![]() 上不是增函数,
上不是增函数,
若![]() 在
在![]() 上是减函数,可得
上是减函数,可得![]() 在区间
在区间![]() 上恒为负值;
上恒为负值;
若![]() 在
在![]() 上是常数函数,可得
上是常数函数,可得![]() 在区间
在区间![]() 上恒为零;
上恒为零;
若![]() 在
在![]() 上是有增有减,可得
上是有增有减,可得![]() 在区间
在区间![]() 上可能为正可能为负;
上可能为正可能为负;
这与![]() 在区间
在区间![]() 上恒为正值矛盾,故
上恒为正值矛盾,故![]() 在
在![]() 上是增函数;
上是增函数;
(3)任意的![]() ,当
,当![]() ,
,
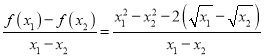
![]() ,
,
构造![]() ;
;
任取![]() ,
,![]() ,
,
![]()
![]()
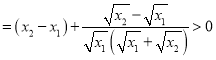 ,
,
![]()
![]()
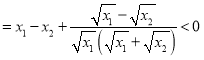 ,
,
故:![]() ,
,
![]()
![]() 是数集
是数集![]() 上
上![]() 的限制函数,
的限制函数,
![]()
![]() ,解得
,解得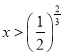
利用(2)结论,当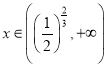 函数单调递增,
函数单调递增,
![]() ,解得
,解得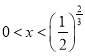
利用(2)结论,当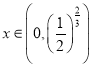 函数单调递减.
函数单调递减.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】如图①在直角梯形ABCP中,![]() ,
,![]() ,
,![]() ,
,![]() ,E,F,G分别是线段PC,PD,BC的中点,现将
,E,F,G分别是线段PC,PD,BC的中点,现将![]() 折起,使平面
折起,使平面![]() 平面ABCD如图②.
平面ABCD如图②.
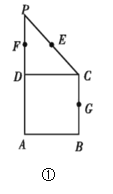
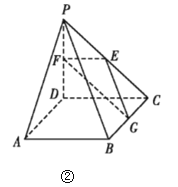
(1)求证:![]() 平面EFG;
平面EFG;
(2)求二面角G—EF—D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在线段![]() 的两端点各置一个光源,已知光源
的两端点各置一个光源,已知光源![]() ,
,![]() 的发光强度之比为
的发光强度之比为![]() ,则线段上光照度最小的一点到
,则线段上光照度最小的一点到![]() ,
,![]() 的距离之比为______(光学定律:
的距离之比为______(光学定律:![]() 点的光照度与
点的光照度与![]() 到光源的距离的平方成反比,与光源的发光强度成正比)
到光源的距离的平方成反比,与光源的发光强度成正比)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国际篮联篮球世界杯,将于2019年在的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传世界杯,某大学从全校学生中随机抽取了![]() 名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
会收看 | 不会收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表说明,能否有![]() 的把握认为收看篮球世界杯赛事与性别有关?
的把握认为收看篮球世界杯赛事与性别有关?
(2)现从参与问卷调查且收看篮球世界杯赛事的学生中,采用按性别分层抽样的方法选取![]() 人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
(i)求男、女学生各选取多少人;
(ii)若从这![]() 人中随机选取
人中随机选取![]() 人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到
人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到![]() 名男生的概率.
名男生的概率.
附: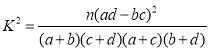 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长为
为边长为![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥
的正方形,△ABE和△BCF均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 在棱
在棱![]() 上,满足
上,满足![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有10名选手参加某项诗词比赛,计分规则如下:比赛共有6道题,对于每一道题,10名选手都必须作答,若恰有![]() 个人答错,则答对的选手该题每人得
个人答错,则答对的选手该题每人得![]() 分,答错选手该题不得分.比赛结束后,关于选手得分情况有如下结论:
分,答错选手该题不得分.比赛结束后,关于选手得分情况有如下结论:
①若选手甲答对6道题,选手乙答对5道题,则甲比乙至少多得1分:
②若选手甲和选手乙都答对5道题,则甲和乙得分相同;
③若选手甲的总分比其他选手都高,则甲最高可得54分
其中正确结论的个数是( )
A.0B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 某创业投资公司拟投资开发某种新能源产品,估计能获得25万元~ 1600万元的投资收益,现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,奖金不超过75万元,同时奖金不超过投资收益的20%.(即:设奖励方案函数模型为y=f (x)时,则公司对函数模型的基本要求是:当x∈[25,1600]时,①f(x)是增函数;②f (x) ![]() 75恒成立;
75恒成立; ![]()
![]() 恒成立.
恒成立.
(1)判断函数![]() 是否符合公司奖励方案函数模型的要求,并说明理由;
是否符合公司奖励方案函数模型的要求,并说明理由;
(2)已知函数![]() 符合公司奖励方案函数模型要求,求实数a的取值范围.
符合公司奖励方案函数模型要求,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com