
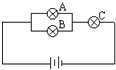
 如图中灯泡A,B,C是否正常是相互独立的,它们不亮的概率分别是0.1,0.2,0.1.
如图中灯泡A,B,C是否正常是相互独立的,它们不亮的概率分别是0.1,0.2,0.1. )=P(
)=P( )•P(
)•P(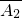 )•P(
)•P( )=(1-0.1)×(1-0.2)×(1-0.1)=0.648
)=(1-0.1)×(1-0.2)×(1-0.1)=0.648 A2A3+A1
A2A3+A1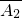 A3)=P(
A3)=P( A2A3)+P(A1
A2A3)+P(A1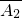 A3)
A3) )=P(
)=P( )•P(
)•P(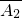 )•P(
)•P( ),代入数据计算即可得到答案
),代入数据计算即可得到答案 A2A3+A1
A2A3+A1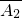 A3)=P(
A3)=P( A2A3)+P(A1
A2A3)+P(A1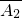 A3)代入数据计算即可得到有灯泡亮也有灯泡不亮的概率
A3)代入数据计算即可得到有灯泡亮也有灯泡不亮的概率

科目:高中数学 来源: 题型:
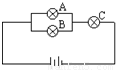
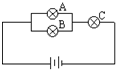 如图中灯泡A,B,C是否正常是相互独立的,它们不亮的概率分别是0.1,0.2,0.1.
如图中灯泡A,B,C是否正常是相互独立的,它们不亮的概率分别是0.1,0.2,0.1.查看答案和解析>>
科目:高中数学 来源:2008-2009学年江苏省无锡一中高二(下)期末数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:安徽省合肥市2010届高三第四次模拟(理) 题型:选择题
从足够多的四种颜色的灯泡中任选六个安置在如右图的6个顶点处,则相邻顶点处灯泡颜色不同的概率为 ( )
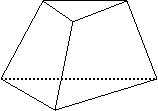 A.
A.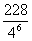 B.
B.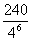 C.
C.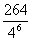 D.
D.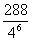
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com