
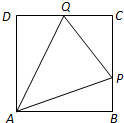
 某生态园要对一块边长为1km的正方形区域ABCD进行规划,设计了如图所示的三条参观路线.具体设计方案如下:从A出发到达BC边上的P点,然后从P点出发到达CD边上的Q点,再直接回到A点,其中要求∠PAQ=45°,设∠PAB=θ,tanθ=t.
某生态园要对一块边长为1km的正方形区域ABCD进行规划,设计了如图所示的三条参观路线.具体设计方案如下:从A出发到达BC边上的P点,然后从P点出发到达CD边上的Q点,再直接回到A点,其中要求∠PAQ=45°,设∠PAB=θ,tanθ=t.| BP |
| AB |
| 1-t |
| 1+t |
| AD2+DQ2 |
1+(
|
| ||
| 1+t |
| 1-t |
| 1+t |
| 2t |
| 1+t |
| 1 |
| 2 |
| 1-t |
| 1+t |
| 1 |
| 2 |
| 2t |
| 1+t |
| 1 |
| 2 |
| 1 |
| 2 |
| t2-2t-1 |
| 1+t |
| 1 |
| 2 |
| t2-2t-1 |
| 1+t |
| 1 |
| 2 |
| (t+1)2-4(t+1)+2 |
| 1+t |
| 1 |
| 2 |
| 2 |
| 1+t |
| 1 |
| 2 |
| 2 |
| 1+t |
| 1 |
| 2 |
(t+1)?
|
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1+t |
| 2 |
| 2 |


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com