
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源:不详 题型:解答题
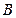 为第一年投资5万元,以后每年都比前一年增加10万元.列出不等式表示“经
为第一年投资5万元,以后每年都比前一年增加10万元.列出不等式表示“经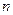 年之后,方案
年之后,方案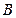 的投入不少于方案
的投入不少于方案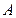 的投入”.
的投入”.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 )2千米,那么这批物资全部运到B市,最快需要_________小时(不计货车的车身长).
)2千米,那么这批物资全部运到B市,最快需要_________小时(不计货车的车身长). 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com