
| lgb |
| lga |
| lga |
| lgc |
| lgb |
| lgc |


科目:高中数学 来源:全优设计必修五数学苏教版 苏教版 题型:044
要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截成三种规格的小钢板的块数如下表所示:
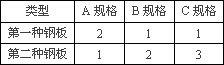
今需要A、B、C三种规格的成品分别为15块、18块、27块,设用第一种钢板x张,第二种钢板y张,怎样写出满足上述所有不等关系的不等式呢?
由题意知:
(1)由两种钢板截得的A种规格的钢板的总块数为________,应________15块;
(2)由两种钢板截得的B种规格的钢板的总块数为________,应________18块;
(3)由两种钢板截得的C种规格的钢板的总块数为________,应________27块.
(4)需截的两种钢板的张数均不能为负.将上述条件用不等式组可表示为________.
查看答案和解析>>
科目:高中数学 来源:训练必修五数学苏教版 苏教版 题型:044
要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截成三种规格的小钢板的块数如下表所示:
今需要A、B、C三种规格的成品分别为15块、18块、27块,设用第一种钢板x张,第二种钢板y张,怎样写出满足上述所有不等关系的不等式呢?
分析:由题意知:
(1)由两种钢板截得的A种规格的钢板的总块数为________,应________15块;
(2)由两种钢板截得的B种规格的钢板的总块数为________,应________18块;
(3)由两种钢板截得的C种规格的钢板的总块数为________,应________27块.
(4)需截的两种钢板的张数均不能为负.将上述条件用不等式组可表示为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com