
(12分)设△ABC的内角A,B,C所对的边分别为a,b,c,且a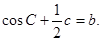
(Ⅰ)求角A的大小;
(Ⅱ)若a=1,求△ABC的周长2的取值范围.
(Ⅰ)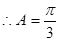 ; (Ⅱ)
; (Ⅱ)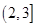 .
.
【解析】本试题主要是考查了解三角形中边角的转化,以及正弦定理和余弦定理的综合运用,三角函数性质的值域问题等等的知识点。
(1)利用正弦定理化变为角,得到关于角A的关系式,然后利用三角方程求解得到
(2)利用正弦定理表示各个边,然后利用周长公式得到关于角的三角函数关系式借助于值域来求解得到范围。
解:(Ⅰ)由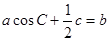 得
得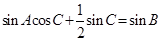
又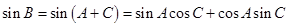
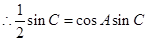 ,
,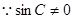 ,
,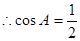 ,
,
又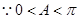
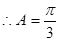 …………………………………………6分
…………………………………………6分
(Ⅱ)由正弦定理得: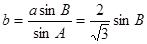 ,
,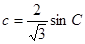
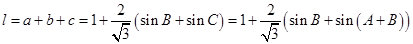

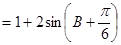
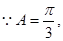
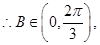
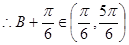

故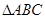 的周长
的周长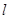 的取值范围为
的取值范围为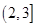 .
…………………………………12分
.
…………………………………12分
(Ⅱ)另解:周长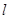
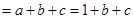
由(Ⅰ)及余弦定理

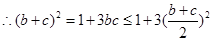
所以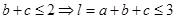
又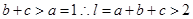
即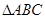 的周长
的周长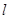 的取值范围为
的取值范围为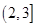 . …………………………………12分
. …………………………………12分


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 5 |
| tanA |
| tanB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| 24 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| x |
| a |
| y |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com