
| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 利用△ABC的面积为$\frac{1}{2}$c2,求出双曲线的渐近线的方程,运用点到直线的距离公式,解方程可得c=$\sqrt{2}$a,
即可求出该双曲线的离心率.
解答 解:设双曲线的一条渐近线方程为y=$\frac{b}{a}$x,
即为bx-ay=0,
则A(a,0)到渐近线的距离为d=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{ab}{c}$,
由题意,△ABC的面积为$\frac{1}{2}$c2,
则$\frac{1}{2}$•2c•$\frac{ab}{c}$=$\frac{1}{2}$c2,
即为4a2b2=c4,
即有4a2(c2-a2)=c4,
即有c2=2a2,
即c=$\sqrt{2}$a,
则e=$\frac{c}{a}$=$\sqrt{2}$.
故选:D.
点评 本题考查双曲线的离心率,考查三角形面积的计算,同时考查点到直线的距离公式的运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
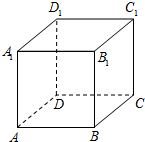 如图,已知正方体ABCD-A1B1C1D,若在其12条棱中随机地取3条,则这三条棱两两是异面直线的概率是$\frac{2}{55}$(结果用最简分数表示)
如图,已知正方体ABCD-A1B1C1D,若在其12条棱中随机地取3条,则这三条棱两两是异面直线的概率是$\frac{2}{55}$(结果用最简分数表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(5,7] | B. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(5,7] | C. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(3,5] | D. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(3,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com