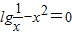练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设x是方程的一个实数根，则x的范围是（ ）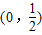
    A．
    B．
    C．（1，2）
    D．（1，+∞）
    【答案】分析：构造函数f（x）=，根据所给的区间，做出区间的两个端点对应的函数值，比较两个端点的函数值，当两个函数值符号相反时，函数的零点就在这一个区间上．
    解答：解：令：f（x）=，
    ∵f（）=lg2-=lg＞0，f（1）=-1＜0，
    f（2）=lg-4＜0，
    ∴f（1）f（）＜0，
    ∴零点所在的区间是（，1）
    故选B．
    点评：本题考查函数的零点的判定定理，是一个基础题，这种题目的运算量比较小，若出现在试卷中是一个送分题目．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设x是任意的一个实数，y表示对x进行四舍五入后的结果，其实质是取与x最接近的整数，在距离相同时，取较大的而不取较小的整数，其函数关系常用y=round（x）表示．例如：round（0.5）=1，round（2.48）=2，round（-0.49）=0，round（-2.51）=-3．
    （1）画出这个函数y=round（x）在区间[-5，5]内的函数图象；
    （2）判断函数y=round（x）（x∈R）的奇偶性，并说明理由；
    （3）求方程round（2x+1）=4x的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设x是任意的一个实数，y表示对x进行四舍五入后的结果，其实质是取与x最接近的整数，在距离相同时，取较大的而不取较小的整数，其函数关系常用y=round（x）表示．例如：round（0.5）=1，round（2.48）=2，round（-0.49）=0，round（-2.51）=-3．
    （1）画出这个函数y=round（x）在区间[-5，5]内的函数图象；
    （2）判断函数y=round（x）（x∈R）的奇偶性，并说明理由；
    （3）求方程round（2x+1）=4x的解集．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年陕西省铜川市耀州中学高一（上）期中数学试卷（解析版） 题型：解答题

    设x是任意的一个实数，y表示对x进行四舍五入后的结果，其实质是取与x最接近的整数，在距离相同时，取较大的而不取较小的整数，其函数关系常用y=round（x）表示．例如：round（0.5）=1，round（2.48）=2，round（-0.49）=0，round（-2.51）=-3．
    （1）画出这个函数y=round（x）在区间[-5，5]内的函数图象；
    （2）判断函数y=round（x）（x∈R）的奇偶性，并说明理由；
    （3）求方程round（2x+1）=4x的解集．

    查看答案和解析>>

    科目：高中数学 来源：0121 期末题 题型：单选题

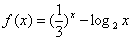    已知函数，设0＜a＜b＜c，且满足f（a）f（b）f（c）＜0，若x0是方程f（x）=0的一个实数解，那么下列不等式中不可能成立的是
    [     ]
    A、x0＜a　 　
    B、x0＞b　 　
    C、x0＜c 　 　
    D、x0＞c

    查看答案和解析>>

    同步练习册答案