将4个半径都是R的球体完全装入底面半径是2R的圆柱形桶中,则桶的最小高度是 .
【答案】
分析:关键弄清桶的取最小高度时,四个球如何放置.由题意知,小球要分两层放置且每层两个,则四个球心构成正四面体,并可求出相对棱的距离.很明显,圆柱的高=上层小球的上方半径R+相对棱间的距离+下层小球的下方半径R.
解答:解:由题意知,小球要分两层放置且每层两个,
令下层两小球的球心分别是A、B,上层两小球的球心分别是C、D.
此时,圆柱底面的半径=两小球半径的和,恰好使小球相外切,且与圆柱母线相切.
圆柱的高=上层小球的上方半径+AB与CD间的距离+下层小球的下方半径=2R+AB与CD间的距离.
令AB、CD的中点分别为E、F.很明显,四面体ABCD每条棱的长都是2R,容易求出:EC=ED、FA=FB,
由EC=ED、CF=DF,得:EF⊥CD.
由FA=FB、AE=BE,得:EF⊥AB.
∴EF是AB与CD间的距离,∴圆柱的高=2R+EF.
由勾股定理,有:CE
2+AE
2=AC
2,CE
2=EF
2+CF
2.
两式相减,消去CE,得:AE
2=AC
2-EF
2-CF
2,
∴EF
2=AC
2-AE
2-CF
2=(2R)
2-R
2-R
2=2R
2,∴EF=
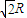
.
∴圆柱的高=2r+

=(2+

)R.
故答案为(2+

)R.
点评:本题考查了,空间位置关系与距离,做题时要弄请存在的等量关系.

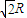 .
. =(2+
=(2+ )R.
)R. )R.
)R.
