
![]() mx + 9m =0的两根,又cos∠BAO =
mx + 9m =0的两根,又cos∠BAO =![]() .
.
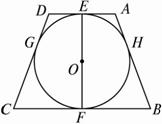
图2-23
(1)求证:AO⊥BO;
(2)求梯形ABCD的面积.
思路分析:(1)运用切线长定理;(2)依据一元二次方程“根与系数的关系”求出m的值,进一步求得AD、BC、EF的长,求出梯形面积.
(1)证明:由切线长定理知OA平分∠DAB,OB平分∠ABC,又∵AD∥BC,∴∠AOB=90°,即AO⊥BO.
(2)解:连结OH,则OH⊥AB.∵cos∠BAO =![]() ,?
,?
∴设OA =3k,AB =5k,OB =4k,?
在Rt△AOH中, ![]() ,
, ![]() ,
, ![]() ,?
,?
由韦达定理得OB +AH =![]() m,OB·AH =9m,?
m,OB·AH =9m,?
即![]() =
=![]() ,4k·5k =9m.?
,4k·5k =9m.?
解之,得k1=5,k2 =0(舍去).?
∴BO =20,AH =9.?
又∵AD =2AH =18,BC =2BF =2BH =32,EF =2OH =24,
即梯形的高EF =24.?
∴S梯形ABCD =![]() ×(18+32)×24=600.
×(18+32)×24=600.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
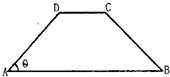 如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,
如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,| π |
| 2 |
| A、随着角度θ的增大,e1增大,e1e2为定值 |
| B、随着角度θ的增大,e1减小,e1e2为定值 |
| C、随着角度θ的增大,e1增大,e1e2也增大 |
| D、随着角度θ的增大,e1减小,e1e2也减小 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是5
如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是5| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=
(2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在等腰梯形ABCD中,AB∥CD且AB=2AD,设∠DAB=θ,θ∈(0,
如图,在等腰梯形ABCD中,AB∥CD且AB=2AD,设∠DAB=θ,θ∈(0,| π | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com