
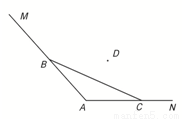
如图,海岸线![]() ,现用长为
,现用长为![]() 的栏网围成一养殖场,其中
的栏网围成一养殖场,其中![]() .
.
(1)若![]() ,求养殖场面积最大值;
,求养殖场面积最大值;
(2)若![]() 、
、![]() 为定点,
为定点,![]() ,在折线
,在折线![]() 内选点
内选点![]() ,使
,使![]() ,求四边形养殖场
,求四边形养殖场![]() 的最大面积;
的最大面积;
(3)若(2)中![]() 、
、![]() 可选择,求四边形养殖场
可选择,求四边形养殖场![]() 面积的最大值.
面积的最大值.
解:(1)设![]()
![]() ,
,
![]() ,
,![]() ,
,
所以,△![]() 面积的最大值为
面积的最大值为![]() ,当且仅当
,当且仅当![]() 时取到.
时取到.
(2)设![]() 为定值).
为定值). ![]() (定值) ,
(定值) ,
由![]() ,a =
,a =![]() l,知点
l,知点![]() 在以
在以![]() 、
、![]() 为焦点的椭圆上,
为焦点的椭圆上,![]() 为定值.
为定值.
只需![]() 面积最大,需此时点
面积最大,需此时点![]() 到
到![]() 的距离最大,
的距离最大,
即![]() 必为椭圆短轴顶点.
必为椭圆短轴顶点.
![]() 面积的最大值为
面积的最大值为![]() ,
,
因此,四边形ACDB面积的最大值为![]() .
.
(3)先确定点B、C,使![]() . 由(2)知
. 由(2)知![]() 为等腰三角形时,四边形ACDB面积最大.
为等腰三角形时,四边形ACDB面积最大.
确定△BCD的形状,使B、C分别在AM、AN上滑动,且BC保持定值,
由(1)知AB=AC时,四边形ACDB面积最大.
此时,△ACD≌△ABD,∠CAD=∠BAD=θ,且CD=BD=![]() .
.
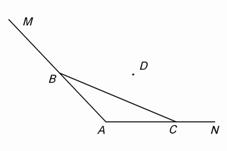
S=![]() .
.
由(1)的同样方法知,AD=AC时,三角形ACD面积最大,最大值为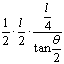 .
.
所以,四边形ACDB面积最大值为![]() .
.


科目:高中数学 来源: 题型:
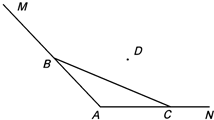 如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.
如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.查看答案和解析>>
科目:高中数学 来源: 题型:
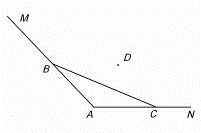 如图,海岸线MAN,∠A=
如图,海岸线MAN,∠A=| 2π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.
如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.查看答案和解析>>
科目:高中数学 来源:2011年江苏省淮安市清河区清江中学高考数学押题卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com