
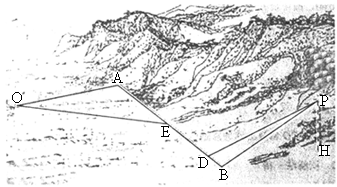
(2007
湖南,19)如图所示,某地为了开发旅游资源,欲修建一条连接风景点P和居民区O的公路.点P所在的山坡面与山脚所在水平面α所成的二面角为θ(0°<θ<90°),且 ,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用.从点O到山脚修路的造价为a万元/km,原有公路改建费用为
,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用.从点O到山脚修路的造价为a万元/km,原有公路改建费用为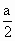 万元/km.当山坡上公路长度为lkm(1≤l≤2)时,其造价为
万元/km.当山坡上公路长度为lkm(1≤l≤2)时,其造价为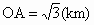 .
.
(1)
在AB上求一点D,使沿折线PDAO修建公路的总造价最小:(2)
对于(1)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小;(3)
在AB上是否存在两个不同的点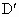 、
、 ,使沿折线
,使沿折线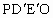 修建公路的总造价小于(2)中得到的最小总造价,证明你的结论.
修建公路的总造价小于(2)中得到的最小总造价,证明你的结论. |
解析: (1)如图PH⊥α,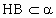 ,PB⊥AB,由三垂线定理逆定理知,AB⊥HB,所以∠PBH是山坡面与α所成二面角的平面角,则∠PBH=θ, ,PB⊥AB,由三垂线定理逆定理知,AB⊥HB,所以∠PBH是山坡面与α所成二面角的平面角,则∠PBH=θ,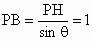 . .
设 BD=x(km),0≤x≤1.5,则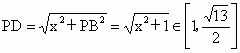 .记总造价为 .记总造价为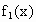 万元.据题设有 万元.据题设有
当 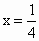 ,即 ,即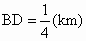 时总造价 时总造价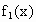 最小. 最小.
(2) 设AE=y(km),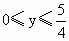 ,总造价为 ,总造价为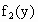 万元,根据题设有 万元,根据题设有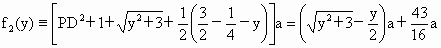 . .
则 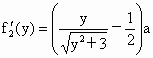 ,由 ,由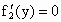 ,得y=1. ,得y=1.
当 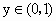 时, 时,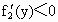 , ,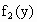 在(0,1)内是减函数; 在(0,1)内是减函数;
当 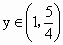 时, 时,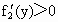 , ,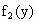 在 在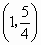 内是增函数. 内是增函数.
故当 y=1,即AE=1(km)时总造价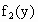 最小,且最小总造价为 最小,且最小总造价为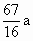 万元. 万元.
(3) 不存在这样的点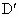 、 、 .事实上,在AB上任取不同的两点 .事实上,在AB上任取不同的两点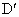 、 、 .为使总造价最小, .为使总造价最小,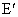 显然不能位于 显然不能位于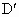 与B之间.故可设 与B之间.故可设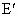 位于 位于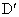 与A之间,且 与A之间,且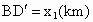 , ,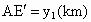 , ,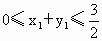 ,总造价为S万元,则 ,总造价为S万元,则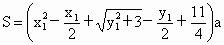 .类似于(1)(2)的讨论知, .类似于(1)(2)的讨论知,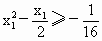 , ,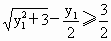 ,当且仅当 ,当且仅当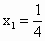 , ,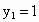 同时成立时,上述两个不等式等号同时成立,此时 同时成立时,上述两个不等式等号同时成立,此时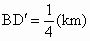 , ,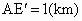 ,S取得最小值 ,S取得最小值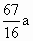 ,点 ,点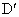 、 、 分别与点D、E重合.所以不存在这样的点 分别与点D、E重合.所以不存在这样的点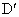 、 、 ,使沿折线 ,使沿折线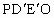 修建公路的总造价小于(2)中得到的最小总造价. 修建公路的总造价小于(2)中得到的最小总造价. |


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com