
已知点 ,
, ,
, ,直线
,直线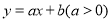 将
将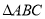 分割为面积相等的两部分,则
分割为面积相等的两部分,则 的取值范围是( )
的取值范围是( )
A.(0, ) B.
) B.  C.
C.  D.
D. 
B
【解析】
试题分析:由题意可得,三角形ABC的面积为 S= 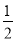 AB•OC=4,由于直线y=ax+b(a>0)与x轴的交点为M(?
AB•OC=4,由于直线y=ax+b(a>0)与x轴的交点为M(? ,0),由题意知?
,0),由题意知? ≤0可得点M在射线OA上.设直线和BC的交点为 N,则由
≤0可得点M在射线OA上.设直线和BC的交点为 N,则由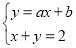 ,可得点N的坐标为
,可得点N的坐标为 ,若点M和点A重合,则点N为线段BC的中点,则?
,若点M和点A重合,则点N为线段BC的中点,则? =-2,且
=-2,且 =1,解得
=1,解得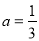 ,
, ,若点M在点O和点A之间,则点N在点B和点C之间,由题意可得三角形NMB的面积等于2,即
,若点M在点O和点A之间,则点N在点B和点C之间,由题意可得三角形NMB的面积等于2,即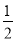 •MB•
•MB•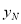 =2,即
=2,即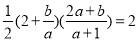 ,解得
,解得 ,故b<1,若点M在点A的左侧,则?
,故b<1,若点M在点A的左侧,则? <-2,b>2a,设直线y=ax+b和AC的交点为P,则由
<-2,b>2a,设直线y=ax+b和AC的交点为P,则由 求得点P的坐标为
求得点P的坐标为 ,此时,
,此时,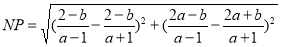
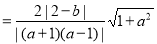 ,此时,点C(0,2)到直线y=ax+b的距离等于
,此时,点C(0,2)到直线y=ax+b的距离等于 ,由题意可得,三角形CPN的面积等于2,即
,由题意可得,三角形CPN的面积等于2,即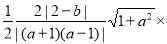
 ,化简可得
,化简可得 ,由于此时 0<a<1,∴
,由于此时 0<a<1,∴ ,两边开方可得
,两边开方可得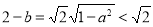 ,则
,则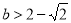 ,综合以上可得b的取值范围是
,综合以上可得b的取值范围是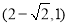 ,答案选B。
,答案选B。

考点:直线方程,三角形面积,不等式的性质


科目:高中数学 来源:2014-2015学年四川省高二上学期10月月考理科数学卷(解析版) 题型:填空题
已知圆 ,直线
,直线 ,给出下面四个命题:
,给出下面四个命题:
①对任意实数 和
和 ,直线
,直线 和圆
和圆 有公共点;
有公共点;
②对任意实数 ,必存在实数
,必存在实数 ,使得直线
,使得直线 与和圆
与和圆 相切;
相切;
③对任意实数 ,必存在实数
,必存在实数 ,使得直线
,使得直线 与和圆
与和圆 相切;
相切;
④存在实数 与
与 ,使得圆
,使得圆 上有一点到直线
上有一点到直线 的距离为3.
的距离为3.
其中正确的命题是 (写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省高二上学期10月月考文科数学卷(解析版) 题型:解答题
(本小题满分12分)设 的内角
的内角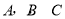 的对边分别为
的对边分别为 ,若角
,若角 为锐角,且
为锐角,且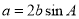 .(1)求
.(1)求 的大小;(2)求
的大小;(2)求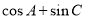 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com