练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如果函数y=2sin2x（x＞0）的图象与直线y=1的交点的横坐标由小到大依次为：x1，x2，x3，…xn，…那么x1+x2+x3+x4+x5+x6+x7=________．


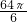
    分析：由已知中函数y=2sin2x（x＞0）的图象与直线y=1的交点的横坐标由小到大依次为：x1，x2，x3，…xn，…我们可以求出满足条件的x的表达式，然后利用分组求和法，我们可以求出答案．
    解答：若函数y=2sin2x=1（x＞0）
    则sin2x=（x＞0）
    则x=kπ+±，k∈N，
    故x1+x2+x3+x4+x5+x6+x7=+++=
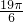
    故答案为：
    点评：本题考查的知识点是正弦函数的图象，其中根据已知条件结合正弦函数的图象和性质，求出满足条件的x的表达式，是解答本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如果函数y=2sin（2x+φ）的图象关于直线x=
    π
    3
    对称，那么|φ|的最小值为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2010•泰安一模）如果函数y=2sin（2x+φ）的图象关于点(
    π
    3
    ，0)    中心对称，那么|φ|的最小值为
    π
    3
    π
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如果函数y=2sin（2x+φ）的图象关于直线数学公式对称，那么|φ|的最小值为


    1. A.
      数学公式
    2. B.
      数学公式
    3. C.
      数学公式
    4. D.
      数学公式

    查看答案和解析>>

    科目：高中数学 来源：泰安一模 题型：填空题

    如果函数y=2sin（2x+φ）的图象关于点(
    π
    3
    ，0)    中心对称，那么|φ|的最小值为______．

    查看答案和解析>>

    科目：高中数学 来源：2010年山东省泰安市高考数学一模试卷（理科）（解析版） 题型：填空题

    如果函数y=2sin（2x+φ）的图象关于点中心对称，那么|φ|的最小值为    ．

    查看答案和解析>>

    同步练习册答案