
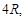 高为
高为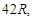 则它最多能放入半径为
则它最多能放入半径为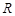 的球 个。
的球 个。科目:高中数学 来源:不详 题型:解答题
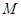 、
、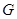 分别是
分别是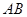 、
、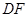 的中点.
的中点.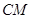
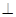 平面
平面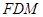
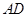 上(含
上(含 、
、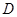 端点)确定一点
端点)确定一点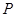 ,使得
,使得
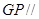 平面
平面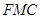 ,并给出证明;
,并给出证明;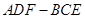 内自由飞,求它飞入几何体
内自由飞,求它飞入几何体 内的概率.
内的概率. 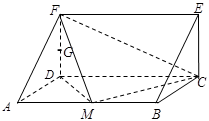
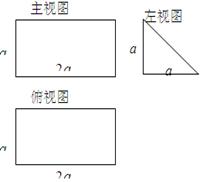
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 三点处,
三点处, ,
, 到线段
到线段 的距离
的距离 ,
, (参考数据:
(参考数据:  ). 今计划建一个生活垃圾中转站
). 今计划建一个生活垃圾中转站 ,为方便运输,
,为方便运输, 准备建在线段
准备建在线段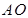 (不含端点)上.
(不含端点)上.
 ,试将
,试将 到三个小区距离的最远者
到三个小区距离的最远者 表示为
表示为 的函数,并求
的函数,并求 的最小值;
的最小值;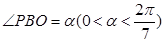 ,试将
,试将 到三个小区的距离之和
到三个小区的距离之和 表示为
表示为 的函数,并确定当
的函数,并确定当 取何值时,可使
取何值时,可使 最小?
最小?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.各个面都是三角形的几何体是三棱锥 |
| B.以三角形一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥 |
| C.棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是六棱锥 |
| D.圆锥的顶点与底面圆周上的任意一点的连线都是母线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com